Câu 1: Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là:
A. 480
B. 24
C. 48
D. 60
Câu 2: Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn một học sinh ở khối 11 đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 45
B. 280
C. 325
D. 605
Câu 3: Một thùng trong đó có 12 hộp đựng bút màu đỏ, 18 hộp đựng bút màu xanh. Số cách khác nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là?
A. 13
B. 12
C. 18
D. 216
Câu 4: Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Số cách khác nhau để chọn được đồng thời một cây bút chì, một cây bút bi và một cuốn tập.
A. 24
B. 48
C. 480
D. 60
Câu 5: Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số đều chẵn ?
A. 99
B. 50
C. 20
D. 10
Câu 6: Từ các chữ số 0; 1;2; 3; 4; 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau ?
A. 154
B. 145
C. 144
D. 155
Câu 7: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?
A. 120
B. 16
C. 12
D. 24
Câu 8: Trên giá sách muốn xếp 20 cuốn sách khác nhau. Có bao nhiêu cách sắp xếp sao cho tập 1 và tập 2 không đặt cạnh nhau.
A. 20! – 18!.
B. 20! – 19!.
C. 20! – 18!.2!.
D. 19!.18!.
Câu 9: Từ các số 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 không đứng cạnh nhau.
A. 410
B. 480
C. 500
D. 512
Câu 10: Sau bữa tiệc, mỗi người bắt tay một lần với mỗi người khác trong phòng. Có tất cả 66 người lần lượt bắt tay. Hỏi trong phòng có bao nhiêu người:
A. 11
B. 12
C. 33
D. 66
Câu 11: Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác
A. 111300
B. 233355
C. 125777
D. 112342
Câu 12: Một nhóm có 5 nam và 3 nữ. Chọn ra 3 người sao cho trong đó có ít nhất 1 nữ. Hỏi có bao nhiêu cách.
A. 54
B. 46
C. 48
D. 40
Câu 13: Một hội nghị bàn tròn có các phái đoàn 3 người Anh, 5 người Pháp và 7 người Mỹ. Hỏi có bao nhiêu cách xếp chỗ ngồi cho các thành viên sao cho những người có cùng quốc tịch thì ngồi gần nhau.
A. 72757640
B. 7293732
C. 3174012
D. Đáp án khác
Câu 14: Có 7 nhà toán học nam, 4 nhà toán học nữ và 5 nhà vật lý nam.Có bao nhiêu cách lập đoàn công tác gồm 3 người có cả nam và nữ đồng thời có cả toán học và vật lý.
A. 210
B. 314
C. 420
D. 213
Câu 15: Cho hai đường thẳng song song d1; d2. Trên đường thẳng d1 lấy 10 điểm phân biệt, trên d2 lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên.
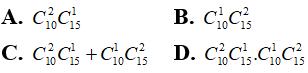
Câu 16: Cho đa giác đều A1A2…A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1, A2, …, An gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1, A2, …, An. Tìm n?
A. 3
B. 6
C. 8
D. 12
Câu 17: Trong khai triển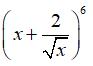 
, hệ số của x3 (x >0) là:
A.60
B.80
C. 160
D. 240
Câu 18: Tìm hệ số của x8 trong khai triển biểu thức sau: h(x) = x(1 – 2x)9
A. – 4608
B. 4608
C. -4618
D. 4618
Câu 19: Tìm số nguyên dương n sao cho: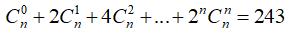 
A. 4
B. 11
C. 12
D. 5
Câu 20: Gieo một con súc xắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là:
Câu 21: Một con súc sắc đồng chất được đổ lần. Xác suất để được một số lớn hơn hay bằng xuất hiện ít nhất lần là
Câu 22: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:
A. 0,24.
B. 0,96.
C. 0,46.
D. 0,92.
Câu 23: Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là 1/5 và 2/7 . Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ”. Khi đó, xác suất của biến cố A là bao nhiêu?
Câu 24: Một hộp đựng 4 viên bi xanh,3 viên bi đỏ và 2 viên bi vàng.Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được 2 viên bi cùng màu
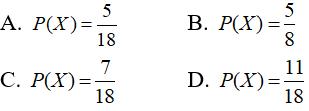
Hướng dẫn giải và Đáp án
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Đáp án | B | D | D | C | C | C | C | D |
| Câu | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Đáp án | B | B | A | B | D | A | C | C |
| Câu | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Đáp án | C | A | D | B | A | C | D | A |
Câu 1:
Nếu chọn một cây bút chì thì sẽ có 8 cách.
Nếu chọn một cây bút bi thì sẽ có 6 cách.
Nếu chọn một cuốn tập thì sẽ có 10 cách.
Theo qui tắc cộng, ta có 8 + 6 +10 = 24 cách chọn.
Chọn đáp án B.
Câu 2:
Nếu chọn một học sinh nam có 280 cách.
Nếu chọn một học sinh nữ có 325 cách.
Theo qui tắc cộng, ta có 280 + 325 = 605 cách chọn.
Chọn đáp án D.
Câu 3:
Để chọn một hộp màu đỏ và một hộp màu xanh, ta có:
Có 12 cách chọn hộp màu đỏ.
Có 18 cách chọn hộp màu xanh.
Vậy theo qui tắc nhân ta có 12. 18 = 216 cách.
Chọn đáp án D.
Câu 4:
Để chọn một cây bút chì – một cây bút bi – một cuốn tập , ta có:
Có 8 cách chọn bút chì.
Có 6 cách chọn bút bi.
Có 10 cách chọn cuốn tập.
Vậy theo qui tắc nhân ta có 8.6.10 = 480 cách.
Chọn đáp án C.
Câu 5:
Gọi số cần tìm có dạng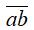 
với (a,b) ∈ A = {0, 2, 4, 6, 8} và a ≠ 0.
Trong đó:
a được chọn từ tập A\{0} nên có 4 cách chọn.
b được chọn từ tập A nên có 5 cách chọn.
Như vậy, ta có 4.5 =20 số cần tìm.
Chọn đáp án C.
Câu 6:
Gọi số cần tìm có dạng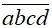 
với (a, b, c, d) ∈ A = {0, 1, 2, 3, 4, 5}.
Vì 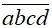là số lẻ ⇒ d ∈ {1, 3, 5} ⇒ d: có 3 cách chọn.
Khi đó, a có 4 cách chọn (khác 0 và d),
b có 4 cách chọn và c có 3 cách chọn.
Vậy có tất cả 3.4.4.3 = 144 số cần tìm.
Chọn đáp án C.
Câu 7:
Xếp An và Dũng ngồi hai đầu ghế có 2! = 2 cách xếp.
Số cách xếp 3 bạn Bình, Chi, Lệ vào 3 ghế còn lại là một hoán vị của 3 phần tử nên có 3!= 6 cách.
Vậy có 2.6 = 12 cách.
Chọn đáp án C.
Câu 8:
Sắp xếp 10 cuốn sách trên giá là một hoán vị của 20 phần tử nên ta có 20! cách sắp xếp.
Khi hai cuốn tập 1 và tập 2 đặt cạnh nhau (thay đổi vị trí cho nhau), ta coi đó là một phần tử và cùng sắp xếp với 18 cuốn sách còn lại trên giá nên có 2.19! cách sắp xếp.
Vậy có tất cả 20! – 2.19! = 19!.18 cách sắp xếp theo yêu cầu bài toán.
Chọn đáp án D.
Câu 9:
Gọi x là số có 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 luôn đứng cạnh nhau.
Đặt y =12 khi đó x có dạng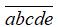 
với a,b,c,d,e đôi một khác nhau và thuộc tập {y, 3, 4, 5, 6} nên có P5 = 5! = 120 số.
Khi hoán vị hai số 1,2 ta được một số khác nên có 120.2 = 240 số x
Vậy số thỏa yêu cầu bài toán là: 6! – 240 = 480 số.
Chọn đáp án B.
Câu 10:
Cứ hai người sẽ có 1 lần bắt tay.
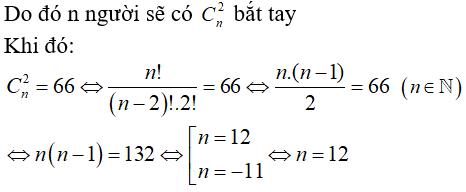
Chọn đáp án B.
Câu 11:
Chọn đáp án A.
Câu 12:
Chọn đáp án B.
Câu 13:
Có 2! cách xếp 3 phái đoàn vào bàn tròn. Với mỗi cách xếp thì có:
3! cách xếp các thành viên phái đoàn Anh
5! cách xếp các thành viên phái đoàn Pháp
7! cách xếp các thành viên phái đoàn Mỹ
Vậy có tất cả: 2!3!5!7! = 7257600 cách xếp.
Chọn đáp án D.
Câu 14:
Chọn đáp án A.
Câu 15:
Chọn đáp án C.
Câu 16:
Số tam giác có các đỉnh là 3 trong 2n điểm A1, A2, …, An là: .
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1, A2, …, An cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1, A2, …, An và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng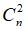 
.
Theo giả thiết:
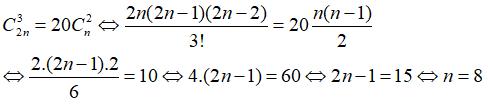
Chọn đáp án C.
Câu 17:
Chọn đáp án C.
Câu 18:
Chọn đáp án A.
Câu 19:
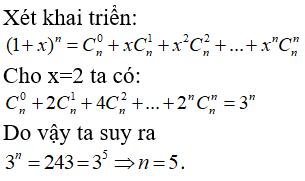
Chọn đáp án D.
Câu 20:
Chọn đáp án B.
Câu 21:
Chọn đáp án A.
Câu 22:
Chọn đáp án C.
Câu 23:
Chọn đáp án D.
Câu 24:
Chọn đáp án A.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây. Chúc các bạn lướt web vui vẻ !
