Tổng hợp bảng giá trị lượng giác
I. Lý thuyết
1. Công thức lượng giác cơ bản
1. tan(x)=sinxcosx2.cot(x)=cosxsinx3. sin2x+cos2x=14. tanx.cot(x)=1 (x≠kπ2, k∈Z)5. 1+tan2x= 1cos2x (x≠π2+kπ, k∈Z)6. 1+cot2(x)= 1sin2(x) (x≠ kπ, k∈Z)
Thơ nhớ hàm lượng giác cơ bản
Sin bình cộng cos bình thì phải bằng 1
Sin bình thì bằng tan bình trên tan bình cộng 1
Cos bình bằng một trên một cộng tan bình
Một trên sin bình bằng 1 cộng cot bình
Một trên cos bình bằng một cộng tan bình
Bắt được quả tan,
Sin nằm trên cos,
Cot cải lại,
Cos nằm trên sin.
Hoặc là:
Bắt được quả tan,
Sin nằm trên cos (tan x = sinxcosx),
Cot dại dột,
Bị cos đè cho (cot x = cosxsinx).
2. Công thức cộng lượng giác
cosx+y=cosxcosy-sinxsinycosx-y=cosxcosy+sinxsinysinx+y=sinxcosy+sinycosxsinx-y=sinxcosy-sinycosxtanx+y=tanx+tany1-tanxtanytanx-y=tanx-tany1+tanxtany
Thơ công thức cộng
Cos cộng cos thì bằng hai cos cos
Cos trừ cos phải bằng trừ hai sin sin
Sin cộng sin thì bằng hai sin cos
Sin trừ sin bằng hai cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin nhớ nha dấu trừ
Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ mà.
3. Công thức các cung liên kết trên đường tròn lượng giác
Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π
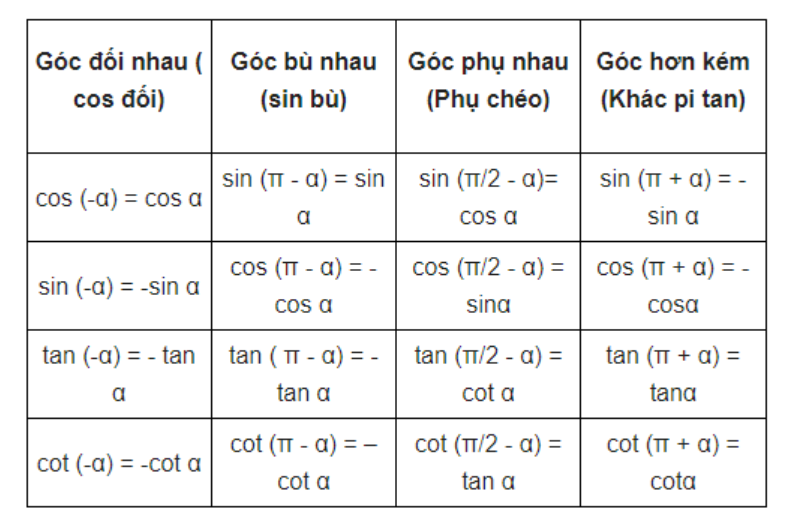
Cung hơn kém π2
+ cos(π2 + x) = – sinx
+ sin(π2 + x) = cosx
4. Công thức nhân
Công thức nhân đôi
cos2x-sin2x= 2cos2x-1=1-2sin2xsin2x=2sinxcosxtan2x=tanx1-tan2x
Công thức nhân ba
sin3x=3sinx-4sin3xcos3x=4cos3x-3cosx
Công thức nhân bốn
8cos4a-8cos2a+1=8sin4a-8sin2a+1
5. Công thức hạ bậc
Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản
Ví dụ như: sin2a=1 – cos2a = 1 – cos2a+12 = 1-cos2a2.
1-cos2x2tan2x=1-cos2x1+cos2x
6. Công thức biến đổi tổng thành tích
1. cosa+cosb=2cosa+b2.cosa-b22. cosa-cosb=-2sina+b2.sina-b23. sina+sinb=2sina+b2.cosa-b24. sina-sinb=2cosa+b2.sina-b25. tana+tanb=sina+bcosa.cosb6. tana-tanb=sina-bcosa.cosb7. sina+cosa=2sina+π4=2cosa-π48. sina-cosa=2sina-π4=-2cosa+π49. tana+cot(a)=2sin(2a)10. cot(a)-tana=2cot(2a)11. sin4a+cos4a=1-12sin22a=14cos4a+3412. sin6a+cos6a=1-34sin22a=38cos4a+58
Thơ nhớ:
Sin tổng lập tổng sin cô.
Cô tổng lập hiệu đôi cô đôi chàng.
Tan tổng thì lập tổng hai tan.
Một trừ tan tích mẫu mang thương sầu.
Gặp hiệu ta chớ phải lo.
Đổi trừ thành cộng ghi sâu trong lòng.
7. Công thức biến đổi tích thành tổng
1.cosacosb=12cosa+b+cosa-b2.sinasinb=-12cosa+b-cosa-b3.sinacosb=-12sina+b-sinsa-b
8. Nghiệm của phương trình lượn giác trong trường hợp đặc biệt
Phương trình lượng giác trong trường hợp đặc biệt:
+ sin a = 0 ⇔ a = kπ; (k ∈ Z)
+ sin a = 1 ⇔ a = π2 + k2π; (k ∈ Z)
+ sin a = -1 ⇔ a = -π2 + k2π; (k ∈ Z)
+ cos a = 0 ⇔ a = π2 + kπ; (k ∈ Z)
+ cos a = 1 ⇔ a = k2π; (k ∈ Z)
+ cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
9. Dấu của các giá trị lượng giác
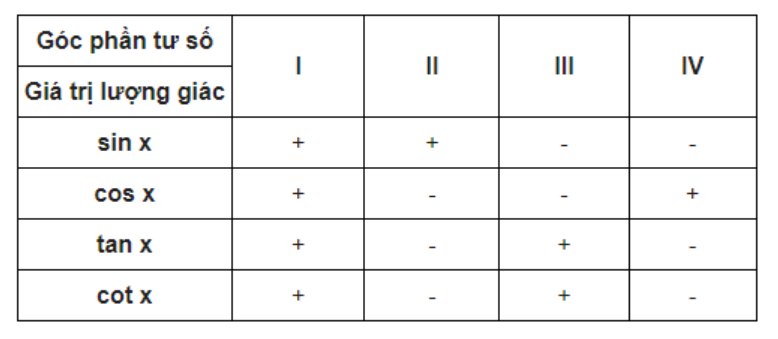
10. Bảng giá trị lượng giác một số góc đặc biệt
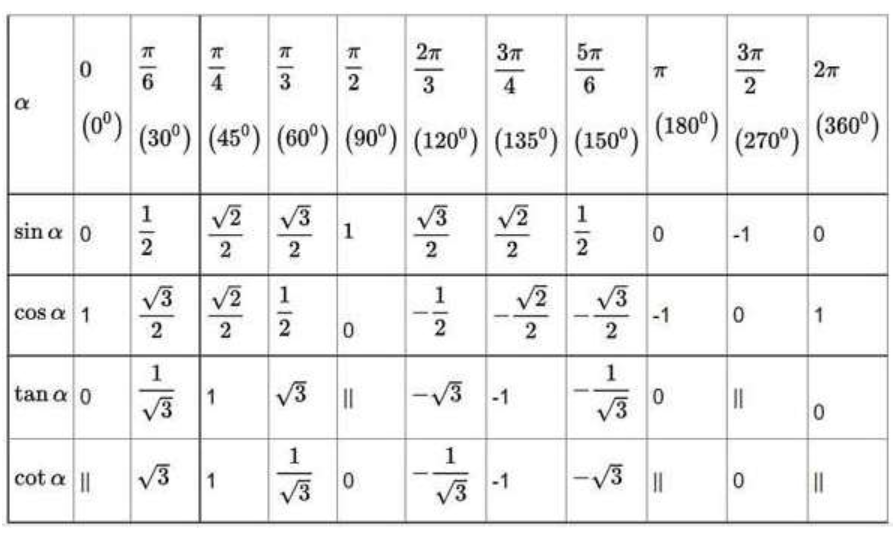
11. Công thức lượng giác bổ sung
Biểu diễn công thức theo t= tana2
1. sina=2t1+t22. cosa=1-t21+t23. tana=2t1-t24. cot(a)= 1-t22t
12. Hàm lượng giác ngược
1. arcsinx+arccosx=π22. arctanx+arccotx=π23. arctanx+ arctan1x=π2, nếu x>0-π2, nếu x<04. arctanx+ arctany=arctanx+y1-xy5. arctanx- arctany=arctanx-y1+xy6. sinarccosx=1-x27. cosarcsinx=1-x28. sinarctanx= x1+x29. cosarctanx= 11+x210. tanarcsinx= x1-x211. tanarccosx=1-x2x
II. Bài tập vận dụng
Câu 1: Cho x+y+z=π, chứng minh rằng: tanx + tany + tanz = tanx . tany . tanz.
Lời giải:
Từ giả thiết, ta có:
x+y+z=π⇔x+y=π−z
⇒tanx+y=tanπ−z
⇔ tanx+tany1−tanx.tany=−tanz
⇔tanx+tany=−tanz+tanx.tany.tanz
⇔tanx+tany+tanz=tanx.tany.tanz
Suy ra đpcm.
Câu 2: Cho sinx+siny=2sinx + y, với x+y≠kπ, k∈ℤ. Chứng minh rằng: tanx2.tany2 = 13.
Lời giải:
Từ giả thiết, ta có:
sinx+siny=2sinx+y⇔2sinx+y2.cosx−y2 =4sinx+y2.cosx+y2
⇔cosx−y2=2cosx+y2 (do x+y≠kπ,k∈ℤ)
⇔cosx2.cosy2 +sinx2.siny2 =2cosx2.cosy2 −sinx2.siny2
⇔3sinx2.siny2=cosx2.cosy2 ⇔tanx2.tany2 = 13
Suy ra đpcm.
Câu 3: Cho sinα=13 với 0<α<π2. Tính giá trị của cosα+π3.
Lời giải:
Ta có: sin2α+cos2α=1⇒cos2α=23⇒cosα=63 (vì 0<α<π2 nên cosα>0).
Ta có: cosα+π3=12cosα−32sinα
=12⋅63−32⋅13=16−12=2−626
Câu 4: Tính giá trị biểu thức M=cos–53°.sin–337°+sin307°.sin113°.
Lời giải:
M=cos–53°.sin–337°+sin307°.sin113°
=cos–53°.sin23°–360°+sin−53°+360°.sin90°+23°
=cos–53°.sin23°+sin−53°.cos23°
=sin23°−53°=−sin30°=−12
Câu 5: Cho số thực α thỏa mãn sinα=14. Tính sin4α+2sin2αcosα.
Lời giải:
Ta có: sin4α+2sin2αcosα
=2sin2αcos2α+2sin2αcosα
=2sin2αcos2α+1cosα
=4sinαcosα1−2sin2α+1cosα
=4sinαcos2α(2−2sin2α)
=4sinα1−sin2α2−2sin2α
=81−sin2α2sinα
=81−1162.14=225128
Câu 6: Rút gọn biểu thức P=cosa+2cos3a+cos5asina+2sin3a+sin5a.
Lời giải:
P=cosa+2cos3a+cos5asina+2sin3a+sin5a
=2cos3acos2a+2cos3a2sin3acos2a+2sin3a
=2cos3acos2a+12sin3acos2a+1
=cos3asin3a=cot3a
Câu 7: Chứng minh biểu thức A=1−tan2x24tan2x−14sin2xcos2x không phụ thuộc vào x.
Lời giải:
Ta có: A=1−tan2x24tan2x−14sin2xcos2x
=1−tan2x24tan2x−14tan2x⋅1cos2x2
=1−tan2x24tan2x−1+tan2x24tan2x
=1−tan2x2−1+tan2x24tan2x
=−4tan2x4tan2x=−1
Vậy biểu thức không phụ thuộc vào biến.
Câu 8: Rút gọn biểu thức A=2cos22α+3sin4α−12sin22α+3sin4α−1 .
Lời giải:
Ta có:
A=2cos22α+3sin4α−12sin22α+3sin4α−1
=cos4α+3sin4α3sin4α−cos4α
=12cos4α+32sin4α32sin4α−12cos4α
=sin4α+30°sin4α−30°
Câu 9: Biến đổi biểu thức sinα−1 thành tích các biểu thức.
Lời giải:
Ta có:
sinα−1=sinα−sinπ2
=2cosα+π22sinα−π22
=2cosα2+π4sinα2−π4.
Câu 10: Biết sinβ=45, 0<β<π2 và α≠kπ. Chứng minh biểu thức: A=3sinα+β−4cosα+β3sinα không phụ thuộc vào α.
Lời giải:
Ta có 0<β<π2sinβ=45⇒cosβ=35
A=3sinα+β−4cosα+β3sinα
=3(sinαcosβ+cosαsinβ)−4(cosαcosβ−sinαsinβ)3sinα
=335sinα+45cosα−435cosα−45sinα3sinα
=5sinα3sinα=53
Vậy biểu thức không phụ thuộc vào biến α.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung giải trí học tập và các kiến thức thú vị khác tại đây.





