Đề kiểm tra học kì 1 môn Toán lớp 11 có đáp án đề số 10

Đề bài

I. TRẮC NGHIỆM (5 điểm)

Câu 1 : Giá trị lớn nhất, nhỏ nhất của hàm số $y = 3 - 2{\cos ^2}x$ lần lượt là:

A. ${y_{\max }} = 3,\,\,{y_{\min }} = 1$.

B. ${y_{\max }} = 1,\,\,{y_{\min }} =  - 1$.

C. ${y_{\max }} = 5,\,\,{y_{\min }} = 1$.

D. ${y_{\max }} = 5,\,\,{y_{\min }} =  - 1$.

Câu 2 : Trong 1 tổ có 6 học sinh nam và 4 học sinh nữ. Chọn ngẫu nhiên 3 bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để 3 bạn được chọn toàn nam?

A. $\dfrac{2}{3}$.                            B. $\dfrac{4}{5}$.   

C. $\dfrac{1}{5}$.                            D. $\dfrac{1}{6}$.   

Câu 3 : Cho hình chóp $S.ABCD$ có đáy là hình thang $ABCD\,\left( {AD//BC} \right)$. Gọi $M$là trung điểm của $CD$. Giao tuyến của hai mặt phẳng $\left( {MSB} \right)$ và $\left( {SAC} \right)$là:

A. $SP$ ($P$là giao điểm của$AB$ và $CD$).      

B. $SO$ ($O$ là giao điểm của$AC$ và $BD$).

C. $SJ$ ($J$là giao điểm của$AM$ và $BD$).

D. $SI$ ($I$ là giao điểm của$AC$ và $BM$).

Câu 4 : Trong mặt phẳng tọa độ $Oxy$, tìm ảnh của đường tròn $\left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4$ qua phép đối xứng trục Ox.

A. $\left( C \right):\,{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 4$.

B. $\left( C \right):\,{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4$.

C. $\left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4$.

D. $\left( C \right):\,{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 2$.

Câu 5 : Nghiệm của phương trình $2\sin x + 1 = 0$ là: 

A. $\left[ \begin{array}{l}x = \dfrac{{ - \pi }}{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.,\,\,k \in Z$.                

B. $x =  \pm \dfrac{{2\pi }}{3} + k2\pi ,\,\,k \in Z$.

C. $x =  \pm \dfrac{\pi }{6} + k2\pi ,\,\,k \in Z$.

D. $\left[ \begin{array}{l}x = \dfrac{\pi }{3} + k2\pi \\x = \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.,\,\,k \in Z$.

Câu 6 : Dãy số $\left( {{u_n}} \right)$ có ${u_n} = \dfrac{n}{{n + 1}}$là dãy số:

A. Giảm.                                            

B. Không tăng, không giảm.

C. Tăng.

D. Không bị chặn.

Câu 7 : Tìm số hạng thứ 11 của cấp số cộng có số hạng đầu bằng 3 và công sai $d =  - 2$.

A. –21.                                     B. 23.

C. -17.                                     D. -19.

Câu 8 : Trong mặt phẳng tọa độ (Oxy), ảnh của điểm $M\left( {1; - 2} \right)$qua phép vị tự tâm O tỉ số $k =  - 2$là:

A. $M'\left( {\dfrac{{ - 1}}{2};1} \right)$.

B. $M'\left( {\dfrac{1}{2};1} \right)$.         
C. $M'\left( {2; - 4} \right)$. 
D. $M'\left( { - 2;4} \right)$.

Câu 9 : Trong mặt phẳng, cho 6 điểm phân biệt sao cho không ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?

A. ${6^3}$.                                        B. ${3^6}$.

C. $A_6^3$.                                       D. $C_6^3$.

Câu 10: Tìm tập xác định của hàm số $y = \tan \,x$.

A. $D = R{\rm{\backslash }}\left\{ {\dfrac{\pi }{4} + k\pi ,\,k \in Z} \right\}$.

B. $D = R{\rm{\backslash }}\left\{ { - \dfrac{\pi }{4} + k\pi ,\,k \in Z} \right\}$.

C. $D = R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,\,k \in Z} \right\}$.    

D. $D = R{\rm{\backslash }}\left\{ {k\pi ,\,k \in Z} \right\}$.

Câu 11 : Trong các mệnh đề sau, mệnh đề nào sai?

A. “Phép vị tự tỉ số $k =  - 1$ là phép dời hình”.

B. “Phép đối xứng tâm biến đường tròn thành đường tròn có cùng bán kính”.

C. “Phép đối xứng trục biến đường thẳng thành đường thẳng song song với nó”.

D. “Phép quay tâm I góc quay ${90^0}$ biến đường thẳng thành đường đường thẳng vuông góc với nó.”         

Câu 12 : Tìm số hạng chứa ${x^3}$ trong khai triển ${\left( {x - \dfrac{1}{{2x}}} \right)^9}$.

A. $C_9^3{x^3}$.

B. $\dfrac{1}{8}C_9^3{x^3}$.

C. $- C_9^3{x^3}$.

D. $- \dfrac{1}{8}C_9^3{x^3}$.

Câu 13 : Nghiệm của phương trình $\sin \,x - \cos 2x = 2$ là:

A. $x =  \pm \dfrac{\pi }{4} + k2\pi ,\,\,k \in Z$.                 

B. $x = k2\pi ,\,\,k \in Z$.

C. $x = \dfrac{\pi }{2} + k2\pi ,\,\,k \in Z$.

D. $x = \dfrac{\pi }{2} + k\pi ,\,\,k \in Z$.

Câu 14 : Cho tứ diện $ABCD$. Gọi $M,\,N$lần lượt là trung điểm của $AB,\,\,AC$. $E$ là điểm trên cạnh $CD$ với $ED = 3EC$. Thiết diện tạo bởi mặt phẳng $\left( {MNE} \right)$ và tứ diện $ABCD$ là:

A. Tam giác $MNE$.            

B. Hình thang $MNEF$ với $F$là điểm trên cạnh$BD$ mà $EF//BC$.

C. Tứ giác $MNEF$với $F$là điểm bất kì trên cạnh $BD$.

D. Hình bình hành $MNEF$với $F$là điểm trên cạnh$BD$ mà $EF//BC$.

Câu 15 : Trong mặt phẳng tọa độ $Oxy$, tìm ảnh của đường thẳng $d:\,x + 2y - 3 = 0$ qua phép tịnh tiến theo $\overrightarrow v \left( {1; - 1} \right)$.

A. $d':\,x + 2y - 2 = 0$

B. $d':\,x + 2y - 4 = 0$.

C. $d':\,x - 2y - 4 = 0$.          

D. $d':\, - x + 2y + 2 = 0$.

Câu 16 : Có bao nhiêu số tự nhiên có 5 chữ số được thành lập từ các chữ số $1,\,2,\,3,\,4,\,5,\,6,\,7,\,8,\,9$.

A. ${5^9}$.                                        B. $C_9^5$.  

C. $A_9^5$.                                       D. ${9^5}$.

Câu 17 : Một hình chóp có tổng số đỉnh và số cạnh bằng 13. Tìm số cạnh của đa giác đáy.

A. 4.                                        B. 3.

C. 5.                                        D. 6.

Câu 18 : Tìm mệnh đề đúng trong các mệnh đề sau

A. Nếu hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha  \right)$đều song song với mọi đường thẳng nằm trong  $\left( \beta  \right)$. 

B. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt $\left( \alpha  \right)$ và $\left( \beta  \right)$ thì $\left( \alpha  \right)$ và $\left( \beta  \right)$ song song với nhau.

C. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.                                      

D. Nếu hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha  \right)$ đều song song với $\left( \beta  \right)$.

Câu 19 : Tìm công bội $q$ của một cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = \dfrac{1}{2}$ và ${u_6} = 16$.

A. $q = 2$.

B. $q = \dfrac{1}{2}$.

C. $q =  - 2$.

D. $q =  - \dfrac{1}{2}$.

Câu 20 : Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Các điểm $I,\,J$ lần lượt là trọng tâm tam giác $SAB,\,SAD$. $M$ là trung điểm $CD$. Chọn mệnh đề đúng trong các mệnh đề sau: 

A. $IJ//\left( {SCD} \right)$.

B. $IJ//\left( {SBD} \right)$.

C. $IJ//\left( {SBC} \right)$.

D. $IJ//\left( {SBM} \right)$.

II. TỰ LUẬN (5 điểm)

Câu 1 (1 điểm) : Giải phương trình sau: ${\sin ^2}x - 3\sin x + 2 = 0$.

Câu 2 (1 điểm) : Đội thanh niên xung kích của một trường phổ thông có 10 học sinh, gồm 4 học sinh lớp A, 3 học sinh lớp B và 3 học sinh lớp C. Hỏi có bao nhiêu cách chọn 5 học sinh đi làm nhiệm vụ mà số học sinh lớp B bằng số học sinh lớp C.

Câu 3 (1 điểm) : Tìm số hạng không chứa $x$ trong khai triển ${\left( {{x^2} + \dfrac{1}{{{x^3}}}} \right)^5}$.

Câu 4 (2 điểm) : Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $N$là trung điểm của cạnh $SC$. Lấy điểm $M$đối xứng với $B$qua $A$.

a) Chứng minh rằng: $MD$ song song với mặt phẳng $\left( {SAC} \right)$.

b) Xác định giao điểm $G$ của đường thẳng $MN$ với mặt phẳng $\left( {SAD} \right)$. Tính tỉ số (\dfrac{{GM}}{{GN}}\).

Lời giải chi tiết

I. TRẮC NGHIỆM

II. TỰ LUẬN

Câu 1 (1 điểm) :

Đặt $t \in \left[ { - 1;1} \right]$

Phương trình đã cho trở thành ${t^2} - 3t + 2 = 0$

$\Leftrightarrow \left[ \begin{gathered} t = 1 \hfill \\ t = 2\,\text{(loại)} \hfill \\ \end{gathered} \right. \Leftrightarrow t = 1$

$\Rightarrow x = \dfrac{\pi }{2} + k2\pi ,\,k \in Z$.  

Câu 2 (1 điểm) :

Số cách chọn 5 học sinh, trong đó: 1 học sinh lớp A, 2 học sinh lớp B, 2 học sinh lớp C là: $C_4^1.C_3^2.C_3^2 = 36$ (cách)

Số cách chọn 5 học sinh, trong đó: 3 học sinh lớp A, 1 học sinh lớp B, 1 học sinh lớp C là: $C_4^3.C_3^1.C_3^1 = 36$ (cách)

Vậy có tất cả số cách chọn5 học sinh đi làm nhiệm vụ mà số học sinh lớp B bằng số học sinh lớp C là: $36 + 36 = 72$ (cách).

Câu 3 (1 điểm) :

Ta có: ${\left( {{x^2} + \frac{1}{{{x^3}}}} \right)^5} = {\left( {{x^2} + {x^{ - 3}}} \right)^5}$$\,= \sum\limits_{i = 0}^5 {C_5^i{{\left( {{x^2}} \right)}^i}.{{\left( {{x^{ - 3}}} \right)}^{5 - i}}}$$\, = \sum\limits_{i = 0}^5 {C_5^i{x^{2i - 15 + 3i}}}  = \sum\limits_{i = 0}^5 {C_5^i{x^{5i - 15}}}$

Số hạng không chứa  trong khai triển ứng với  thỏa mãn: $5i - 15 = 0 \Leftrightarrow i = 3$

Số hạng không chứa $x$ trong khai triển là: $C_5^3 = 10$.

Câu 4 (2 điểm) :

 

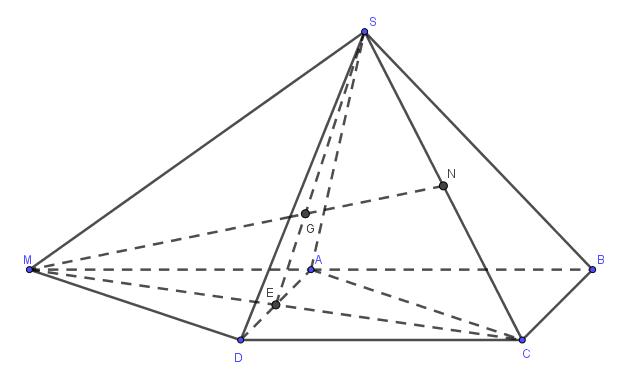
a) 

Do là hình bình hành nên $\overrightarrow {AB}  = \overrightarrow {DC}$, mà M đối xứng với B qua A

$\Rightarrow \overrightarrow {AB}  = \overrightarrow {MA}  \Rightarrow \overrightarrow {DC}  = \overrightarrow {MA} $ $\Rightarrow ACDM$ là hình bình hành $\Rightarrow MD//AC$ 

Vì $AC \subset \left( {SAC} \right) \Rightarrow MD//\left( {SAC} \right)$.

b) Gọi E là giao điểm của AD và MC. Do ACDM là hình bình hành nên  là trung điểm của MC

Trong (SMC) gọi G là giao điểm của SE và MN $ \Rightarrow \left\{ \matrix{ G \in MN \hfill \cr G \in SE \hfill \cr}  \right.$ 

Mà $SE \subset \left( {SAD} \right) \Rightarrow G = MN \cap \left( {SAD} \right)$

Tam giác SMC có: SE, MN là trung tuyến,$SE \cap MN = G$

$\Rightarrow$ G là trọng tâm tam giác SMC $\Rightarrow \dfrac{{MG}}{{GN}} = \dfrac{2}{1} = 2$.