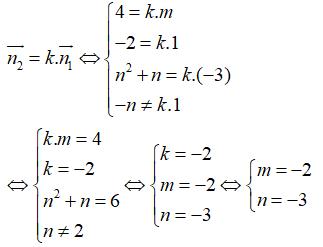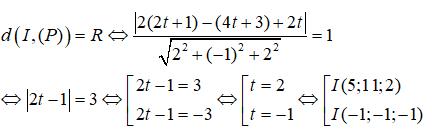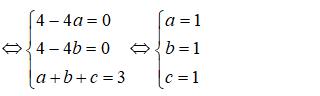Bài tập Toán 12 ôn tập cuối năm phần hình học có lời giải P2 với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng sẽ giúp học sinh ôn trắc nghiệm Toán Hình 12. Qua đó giúp cải thiện kĩ năng và tư duy làm bài góp phần cải thiện kết quả học tập. Mời các bạn tham khảo.
Câu 21: Trong không gian Oxyz, cho hai điểm A(3;2;1), M(3;0;0) và mặt phẳng (P) có phương trình là: x + y + z – 3 = 0 . Viết phương trình của đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ A đến đường thẳng d nhỏ nhất
A. x = -3 – t, y = t, z = 0 C. x = 3 – t, y = t, z = 0
B. x = 3 + t, y = 2t, z = 2t D. Đáp án khác
Đáp án chi tiết :
Gọi H là hình chiếu của A trên đường thẳng d.
Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến np→(1; 1; 1) . AM→(0; -2; -1) Đường thẳng d nhận vecto [AM→;np→] làm vecto chỉ phương. Phương trình tham số của d:
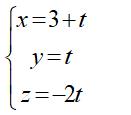
Chọn D
Câu 22: Cho một đồ chơi hình khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = 6cm. Trong tất cả các khối cầu có thể chứa đồ chơi đó thì khối cầu có bán kính nhỏ nhất là:
A. √6 (cm) B. 2√6 (cm) C. 3√3 (cm) D. 3√6 (cm)
Đáp án chi tiết :
Chọn hệ trục tọa độ Oxyz; trong đó điểm S(0; 0; 0); A(6; 0; 0); B(0; 6; 0) và C(0; 0; 6).
Tam giác ABC là tam giác đều: AB = BC = AC = 6√2
Xét mặt cầu tâm I, là tâm của tam giác đều ABC, và có bán kính r = 2√6, bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Do I là tâm tam giác ABC nên I(2; 2; 2).
Khoảng cách 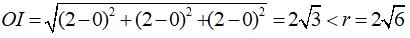
Lưu ý. Lỗi thường gặp là chọn đáp án C vì đó là bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
Câu 23: Trong không gian Oxyz, cho các điểm A(1;1;0), B(0;1;1). Tìm trên mặt phẳng xOz tọa độ điểm C để OABC là một tứ diện đều
A. C(0;0;1) B. C(1;0;0) C. C(1;0;1) D. C(2;0;2)
Đáp án chi tiết :
Dựng hình lập phương cạnh bằng 1, nhận O, A, B, C làm các đỉnh.
Câu 24: Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2 + y2 + z2 = 1. Viết phương trình mặt phẳng (P) đi qua
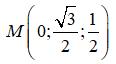
và tiếp xúc với (S)
A. √3x + 4z – 2 = 0 C. y + √3z = 0
B. √3y + z – 2 = 0 D. x + √3y + z – 2 = 0
Đáp án chi tiết :

Câu 25: Trong không gian Oxyz, cho ba điểm A(1; -2; 3), B(0; 1; 5), C(4; -1; 7). Gọi M là trung điểm của BC. Viết phương trình tham số của đường thẳng AM
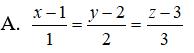
B. x = -1 + t, y = 2 + 2t, z = -3 + 3t
C. x = 1 + t, y = 2 – 2t, z = 3 + 3t
D. x = 1 + t, y = -2 + 2t, z = 3 + 3t
Đáp án chi tiết :

Câu 26: Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 = 0
A. x = -1 – 3t, y = -2 – t, z = 3 C. x = 3 + t, y = 1 + 2t, z = -3t
B. x = 1 + 3t, y = 2 + t, z = -3 + t D. x = 1 + 3t, y = 2 + t, z = -3
Đáp án chi tiết :
Mặt phẳng (P) có vecto pháp tuyến là: np→(3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: ud→ = np→(3; 1; 0)
Phương trình tham số của đường thẳng d:
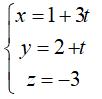
Chọn D.
Câu 27: Trong không gian Oxyz, viết phương trình của mặt phẳng (P) chứa hai đường thẳng sau: d1: x = 3 + 4t, y = 1 – 2t, z = 3 + 6t và
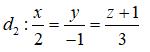
A. 7x + y – 5z – 5 = 0 C. 2x – y + 3z + 3 = 0
B. 7x – y – 5z – 5 = 0 D. 3x + y + 3z – 5 = 0Hiển thị đáp án

Câu 28: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)
A. x + 1 = 0 C. y + z – 1 = 0
B. x – 1 = 0 D. x = 1 + t, y = -2, z = 3
Đáp án chi tiết :
* Tam giác ABC có MN là đường trung bình nên MN// BC (1)
Tam giác ACD có NP là đường trung bình nên NP // CD (2)
Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).
* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là i→(1; 0; 0) nên mặt phẳng (MNP) có VTPT i→(1; 0; 0).
* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).
* Phương trình mặt phẳng (MNP) là:
1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0
Chọn B.
Câu 29: Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình là:
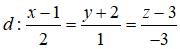
(P): 2x + y – 3z – 4 = 0. Trong những khẳng định dưới đây, khẳng định nào đúng?
A. d nằm trong mặt phẳng (P) C. d không vuông góc với mặt phẳng (P)
B. d song song với mặt phẳng (P) D. d cắt mặt phẳng (P)
Đáp án chi tiết :
Ta có vectơ chỉ phương của đường thẳng d là : ud→ = (2; 1; -3), đồng thời nP→ = (2; 1; -3) = ud→ cũng là vectơ pháp tuyến của mặt phẳng (P). Do đó đường thẳng d vuông góc với mặt phẳng (P), suy ra đường thẳng d cắt mặt phẳng (P).
Câu 30: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6), B(1;1;1), C(0;3;0), D(0;0;3). Viết phương trình tham số của đường thẳng d chứa đường cao AH của tứ diện ABCD
A. x = 2 + t, y = -4 – t, z = 6 + t C. x = 2 + t, y = -4 + t, z = 6 + t
B. x = 1 + 2t, y = -1 -4t, z = 1 + 6t D. x = 1 + 2t, y = 1 – 4t, z = 1 + 6t
Đáp án chi tiết :

Câu 31: Trong không gian Oxyz, cho hai đường thẳng cắt nhau:d1: x = 1 + t, y = 1, z = 1 – t, d2: x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng d1, d2
A. x + y + z – 3 = 0 C. x – y + z – 1 = 0
B. x + y + z + 3 = 0 D. x – y + z + 1 = 0
Đáp án chi tiết :
Đường thẳng d1 đi qua A(1; 1; 1), vecto chỉ phương u1→(1; 0; -1)
Đường thẳng d2 đi qua B( 0; 2;1), vecto chỉ phương u2→(-1; 1; 0)
Mặt phẳng (P) chứa hai đường thẳng d1; d2 nên nhận vecto [u1→;u2→] = (1; 1; 1) làm vecto pháp tuyến và đi qua A(1; 1; 1). Phương trình (P):
1(x – 1) + 1(y – 1) + 1(z – 1) = 0 hay x + y + z – 3= 0
Chọn A.
Câu 32: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y – 3z + 1 = 0; 4x – 2y + (n2 + n)z – n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau
A. m=-2 và n=2 C. m=-2 và n=2 hoặc n=-3
B. m=2 và n=-3 D. m=-2 và n=-3
Đáp án chi tiết :
Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho :
Câu 33: Trong không gian Oxyz, cho đường thẳng
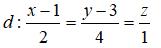
và mặt phẳng (P): 2x – y + 2z = 0. Cho mặt cầu (S) có tâm I thuộc đường thẳng d, có bán kính bằng 1 và tiếp xúc với mặt phẳng (P). Tọa độ tất cả các điểm I có thể là:
A. I1(5; 11; 2) C. I2(3; 7; 1) hoặc I3(-3; -5; -2)
B. I2(3; 7; 1) D. I1(5; 11; 2) hoặc I4(-1; -1; -1)
Đáp án chi tiết :
Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t
Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có :
Câu 34: Trong không gian Oxyz, lập phương trình của mặt cầu (S) đi qua 3 điểm O, A(2;0;0), B(0;2;0) và tâm thuộc mặt phẳng (P): x + y + z – 3 = 0
A. (x – 1)2 + (y – 1)2 + (z – 1)2 = 3 C. (x – 1)2 + (y – 1)2 + (z – 1)2 = 9
B. (x + 1)2 + (y + 1)2 + (z + 1)2 = 3 D. (x + 1)2 + (y + 1)2 + (z + 1)2 = 9
Đáp án chi tiết :
Gọi I(a,b,c) là tâm của mặt cầu (S). Ta có: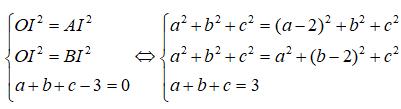
=> I(1; 1; 1); R = OI = √3
Vậy phương trình của mặt cầu (S) là: (x – 1)2 + (y – 1)2 + (z – 1)2 = 3
Câu 35: Trong không gian Oxyz, cho bốn điểm A(1;0;0), B(0;-2;0), C(0;0;2), M(1;1;4). Tính khoảng cách từ M đến mặt phẳng (ABC)
A. 0 B. √6/2 C. 1/2 D. 2
Đáp án chi tiết :

Câu 36: Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – y – 2z + 7 = 0, (Q): 2x – y – 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
A. 4π B. π C. 2π D. 16π
Đáp án chi tiết :
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n→(2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
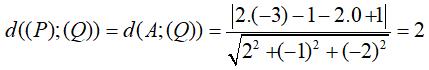
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu:
2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4πR2 = 4 π
Câu 37: Trong không gian Oxyz, cho hai đường thẳng:
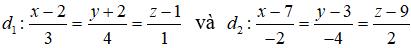
Cho M là một điểm di động trên d1 , N là một điểm di động trên d2 . Khoảng cách nhỏ nhất của đoạn thẳng MN là:
Đáp án chi tiết :
* Với M là một điểm di động trên d1 , N là một điểm di động trên d2 thì MN ≤ d(d1; d2)
Do đó, khoảng cách nhỏ nhất của MN chính là khoảng cách giữa hai đường thẳng d1 và d2. Khi đó, MN là đoạn vuông góc chung của hai đường thẳng đã cho.
* Đường thẳng d1 đi qua A(2; -2; 1), vecto chỉ phương u1→(3; 4; 1)
Đường thẳng d2 đi qua B(7;3;9) vecto chỉ phương u2→(-2; -4; 2)
Ta có:
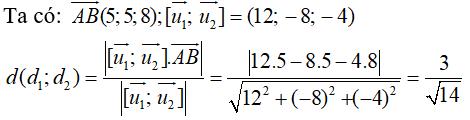
Chọn B.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây.