Câu 1: Khai triển biểu thức (x-m2)4 thành tổng các đơn thức:
A. x4 –x3m+x2m2 + m4
B. x4 –x3m2+x2m4 –xm6+ m8
C. x4 –4x3m+6x2m2 -4xm+ m4
D. x4 –4x3m2+6x2m4 – 4xm6+ m8
Hiển thị đáp án
Sử dụng nhị thức Niuton với a = x, b = – m2
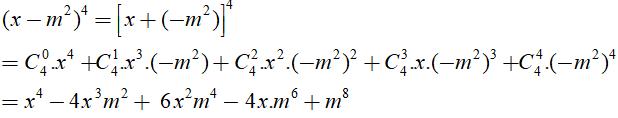
Chọn đáp án D
Câu 2: Tìm số hạng không chứa x trong khai triển
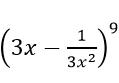
A. 2268 B. -2268
C. 84 D. -27
Hiển thị đáp án

Chọn đáp án là B
Câu 3: Xác định hệ số của số hạng chứa x3 trong khai triển (x2-2/x)n nếu biết tổng các hệ số của ba số hạng đầu trong khai triển đó bằng 49.
A. 160 B. -160
C. 160x3 D. -160x3
Hiển thị đáp án
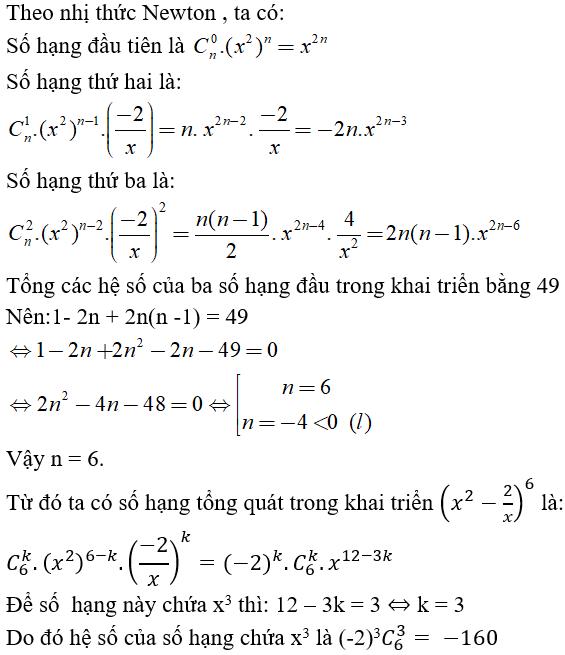
Chọn đáp án là B
Câu 4: Tính tổng S = 32015.C2015o-32014C20151+32013C20152-…+3C20152014 -C20152015
A. 22015 B. -22015
C. 32015 D. 42015
Hiển thị đáp án
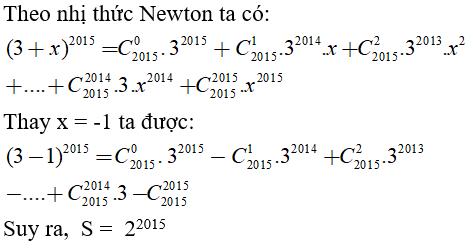
Chọn đáp án A
Câu 5: Trong khai triển nhị thức (a + 2)n + 6, (n ∈ N). Có tất cả 17 số hạng. Vậy n bằng:
A. 17
B. 11
C. 10
D. 12Hiển thị đáp án
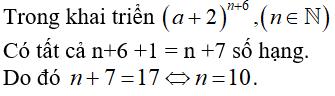
Chọn đáp án C
Câu 6: Tìm hệ số của x12 trong khai triển (2x – x2)10

Hiển thị đáp án

Chọn đáp án B
Câu 7: Tìm số hạng chứa x3 trong khai triển 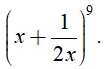

Hiển thị đáp án
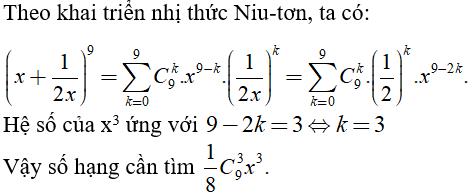
Chọn đáp án B
Câu 8: Tìm số hạng đứng giữa trong khai triển (x3 + xy)21
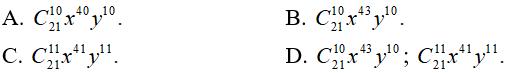
Hiển thị đáp án
Theo khai triển nhị thức Niu-tơn, ta có
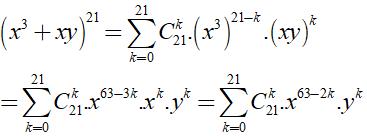
Suy ra khai triển (x 3 + xy) 21 có 22 số hạng nên có hai số hạng đứng giữa là số hạng thứ 11 (ứng với k = 10) và số hạng thứ 12 (ứng với k = 11). Vậy hai số hạng đứng giữa cần tìm là
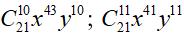
.
Chọn đáp án D
Câu 9: Tìm hệ số của x5 trong khai triển P(x) = x(1 – 2x)5 + x2(1 + 3x)10
A. 80
B. 3240
C. 3320
D. 259200
Hiển thị đáp án

Chọn đáp án C
Câu 10: Tìm hệ số của x5 trong khai triển : P(x) = (1 + x) + 2(1 + x)2 + … + 8(1 + x)8.
A. 630
B. 635
C. 636
D.637
Hiển thị đáp án
Các biểu thức (1 + x), (1 + x)2, ⋯, (1 + x)4 không chứa số hạng chứa x5.

Chọn đáp án C
Câu 11: Tìm số nguyên dương n thỏa mãn 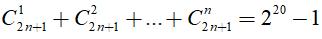 .
.
A.n = 8
B.n = 9
C.n = 10
D. n = 11
Hiển thị đáp án

Chọn đáp án C
Câu 12: Tìm số nguyên dương n thỏa mãn 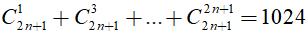 .
.
A.n = 5
B.n = 9
C.n = 10
D.n = 4
Hiển thị đáp án

Chọn đáp án A
Câu 13: Tìm số nguyên dương n sao cho: 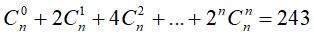
A. 5
B. 11
C. 12
D. 4
Hiển thị đáp án
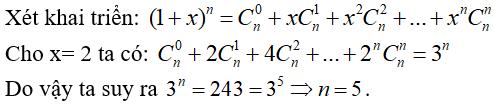
Chọn đáp án A
Câu 14: Tính 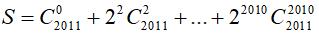
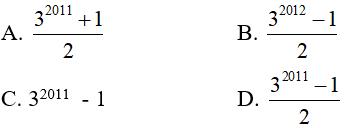
Hiển thị đáp án
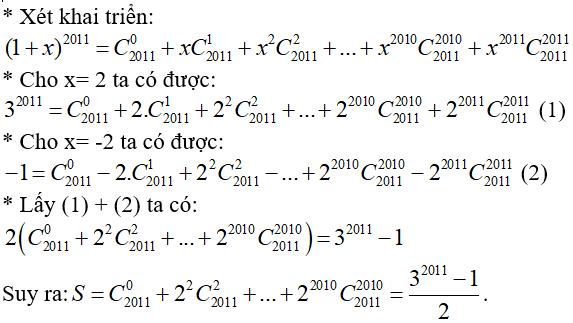
Chọn đáp án D
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây. Chúc các bạn lướt web vui vẻ !




