Câu 1: Hàm số y= 3tan( 2x – π/6) có tập xác định là:
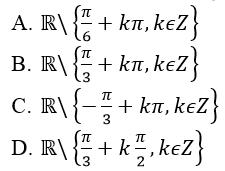
Hiển thị đáp án
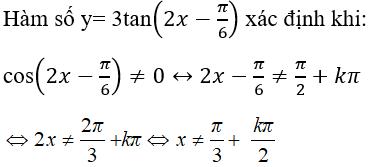
Chọn đáp án D
Câu 2: Hàm số
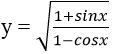
có tập xác định là:
Hiển thị đáp án
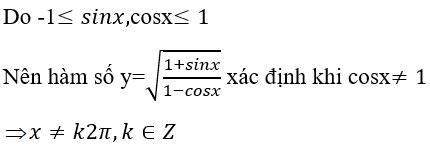
Chọn đáp án C
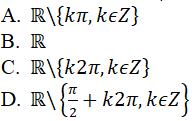
Câu 3: Hàm số
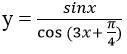
có tập xác định:
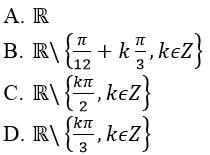
Hiển thị đáp án

Chọn đáp án B
Câu 4: Cho hàm số y = tanx – cotx. Khoảng mà hàm số xác định là:
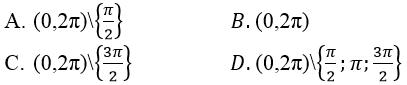
Hiển thị đáp án
Điều kiện xác định của hàm số là:
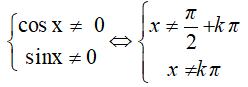
Do đó, hàm số đã cho xác định trên khoảng phương án D. Các phương án A, B, C đều không xác định.
Chọn đáp án D
Câu 5: Hãy chỉ ra hàm số chẵn trong các hàm số sau:
A. y = sinx B. y= sinx + cotx
C. y= sin(π/2-x) D. y= sinx.cos2x
Hiển thị đáp án
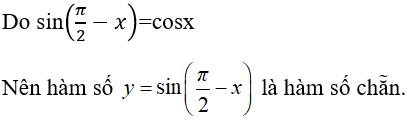
Chọn đáp án C
Câu 6: Hãy chỉ ra hàm số lẻ trong các hàm số sau:
A. y= cos2x.cos(π/2-x) B. y= sin2xcosx
C. y= sinx – cosx D. y= xsinx
Hiển thị đáp án

Chọn đáp án A
Câu 7: Hàm số nào sau đây không có tính chẵn, lẻ?
A. y= cos2xcos(π/2-x) B. y= sin2x.cosx
C. y= sinx – cosx D. y= x.sinx
Hiển thị đáp án
Xét phương án C: y = f(x)= sinx – cosx
Ta có: f(-x) = sin(-x) – cos(-x) = – sinx – cosx
Và – f(x) = – sinx + cos x.
Do đó, f(x) ≠ f(-x); f(-x) ≠ -f(x)
Nên hàm số này không chẵn không lẻ.
Chọn đáp án C
Câu 8: Cho hàm số y= 2sinx/2, hãy chỉ ra mệnh đề sai trong bốn mệnh đề sau:
A. Hàm số đã cho là hàm số lẻ
B. Hàm số đã cho có giá trị lớn nhất bằng 2
C. Hàm số đã cho có chu kì 4π
D. Trong ba mệnh đề trên có ít nhất một mệnh đề sai
Hiển thị đáp án

Chọn đáp án D
Câu 9: Hãy chỉ ra hàm số tuần hoàn trong các hàm số sau:
A. y= xsinx B. y= sin3x
C. y= x – sinx D. y= x/(2+sinx)
Hiển thị đáp án
Hàm số y = sin3x tuần hoàn với chu kì 2π/3
Chọn đáp án B
Câu 10: Chu kì của hàm số y = tan x/2 là:
A. 2π B. 4π
C. π D. π/2
Hiển thị đáp án
Chu kì của hàm số 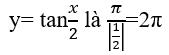
Chọn đáp án A
Câu 11: Chu kì của hàm số y = sin5x là:
A. 2π B. 5π
C. 10π D. 2π/5
Hiển thị đáp án
Chu kì của hàm số y = sin5x là 2π/5
Chọn đáp án D
Câu 12: Chu kì của hàm số y = sinx/3 là
A. 2π B. 6π
C. π/3 D. 2π/3
Hiển thị đáp án
Chu kì của hàm số 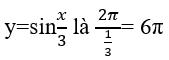
Chọn đáp án B
Câu 13: Chu kì của hàm số y = cosx/2+sinx là:
A. 0 B. 2π
C. 4π D. 6π
Hiển thị đáp án
Chu kì của hàm số y = cos x/2 là 4π, của hàm số y = sinx là 2π.
Vậy chu kì của hàm số đã cho là 4π
Chọn đáp án C
Câu 14: Số phần tử thuộc tập nghiệm của phương trình tan3x= √3 trong khoảng [0;2π} là:
A. 2 B. 3
C. 4 D. 6
Hiển thị đáp án
Ta có:
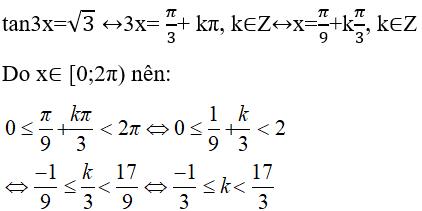
Mà k nguyên nên k ∈ {0; 1; 2; 3; 4; 5}
Tương ứng 6 giá trị của k là 6 nghiệm thỏa mãn đầu bài.
Chọn đáp án D
Câu 15: Số phần tử thuộc tập nghiệm của phương trình 4sinx = 1/sinx trong khoảng [0;2π}
A. 2 B. 3
C. 6 D. 4
Hiển thị đáp án
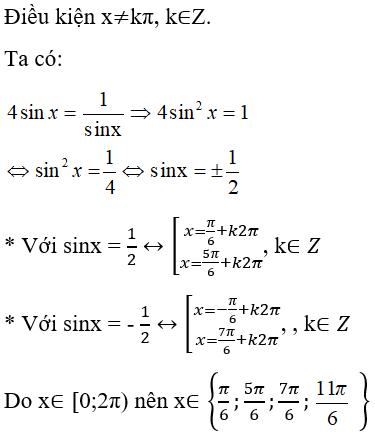
Chọn đáp án D
Câu 16: Trong các phương trình sau, phương trình nào vô nghiệm?
A. sinx+ 3 = 0 B. 2cos2x -cosx – 1 = 0
C. tanx + 3 = 0 D. 3sinx – 2 = 0
Hiển thị đáp án
Phương trình sinx = a có nghiệm
⇔ -1 ≤ a ≤ 1
Xét phương trình sinx + 3= 0
⇔ sinx = -3 ∉ [-1; 1]
Do đó, phương trình này vô nghiệm.
Chọn đáp án A
Câu 17: Tập nghiệm của phương trình sinxcos2x= 0 là:
A. {kπ, k∈Z} B. {π/2+kπ,k∈Z}
C. {k2π,k∈Z} D. Kết quả khác
Hiển thị đáp án
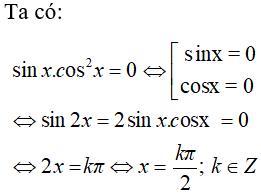
Chọn đáp án D
Câu 18: Nghiệm của phương trình sin3x – cosx = 0 là:
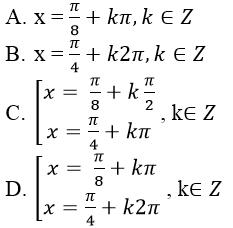
Hiển thị đáp án
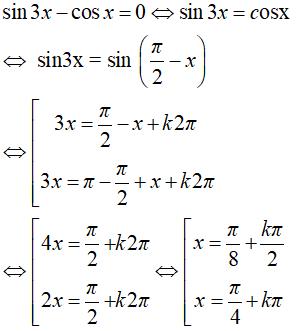
Chọn đáp án C
Câu 19: Giá trị lớn nhất của hàm số y = 3sinx + 4cosx là:
A. 3 B. 4
C. 5 D. 7Hiển thị đáp án
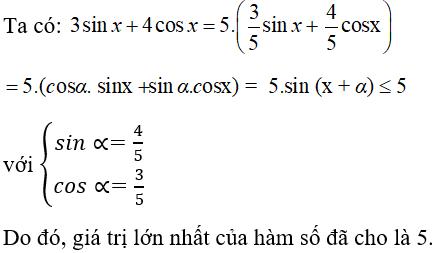
Chọn đáp án C
Câu 20: Giá trị nhỏ nhất của hàm số y = 2 + sinxcosx là:
A. 1 B. 3/2
C. 2 D. Một số khácHiển thị đáp án
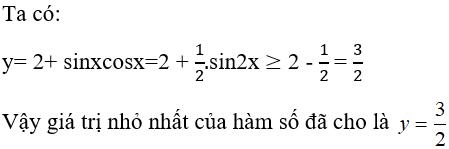
Chọn đáp án B
Câu 21: Tổng các nghiệm của phương trình
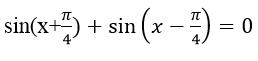
thuộc khoảng (0;4π) là:
A. 2π B. 6π
C. 9π D. 10π
Hiển thị đáp án

Chọn đáp án B
Câu 22: Phương trình cos(πcos2x) = 1 có nghiệm là:
A. x=π/4+kπ,k∈Z B. x=π/4+k π/2,k∈Z
C. x=π/2+kπ,k∈Z D. x=0
Hiển thị đáp án
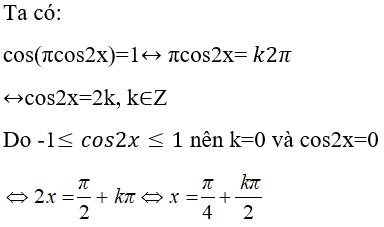
Chọn đáp án B
Câu 23: Tập nghiệm của phương trình sin23x – 3sin3x + 2 = 0 là:
A. {π/2+k2π,k∈Z} B. {π/6+k2π,k∈Z}
C. {π/6+k π/3,k∈Z} D. {π/6+k2 π/3,k∈Z}Hiển thị đáp án
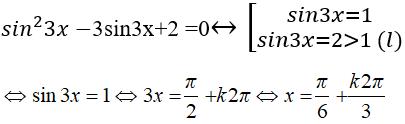
Chọn đáp án D
Câu 24: Tập nghiệm của phương trình sin4x – 13sin2x + 36 = 0 là:
A. {k2π,k∈Z} B. {π/4+k2π,k∈Z}
C. {±π/4+k2π,k∈Z} D. ∅
Hiển thị đáp án
Đặt t= sin2x;
Khi đó, phương trình đã cho trở thành:
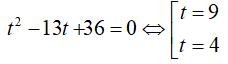
Đối chiếu điều kiện, suy ra không có giá trị nào của t thỏa mãn. Nên phương trình đã cho vô nghiệm.
Chọn đáp án D
Câu 25: Phương trình 2sin2x – 5sinxcosx – cos2x + 2 = 0 có cùng tập nghiệm với phương trình nào trong số bốn phương trình sau:
A. 4sin2x – 5sinxcosx -cos2x = 0
B. 4sin2x + 5sinxcosx + cos2x = 0
C. 4tan2x – 5tanx + 1 =0
D. 5sin2x + 3cos2x = 2
Hiển thị đáp án
Ta có:
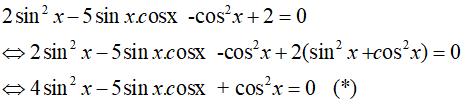
* Lại có, cos x =0 không là nghiệm của phương trình trên .
Chia cả hai vế cho cos2x ta được: 4tan2x – 5tanx + 1 = 0
Chọn đáp án C
Câu 26: Tập nghiệm của phương trình sin2x – √3sinxcosx + cos2x = 0 là:
A. {π/6+kπ,k∈Z} B. {π/2+kπ,k∈Z}
C. {π/6+kπ,π/2+kπ,k∈Z} D. {π/2+k2π,k∈Z}
Hiển thị đáp án

Chọn đáp án C
Câu 27: Tập nghiệm của phương trình sin15x + cos14x = 1 là:
A. {k2π,π/2+k2π;k∈Z} B. {kπ,π/2+k2π;k∈Z}
C. {π/2+k2π;k∈Z} D. ∅
Hiển thị đáp án
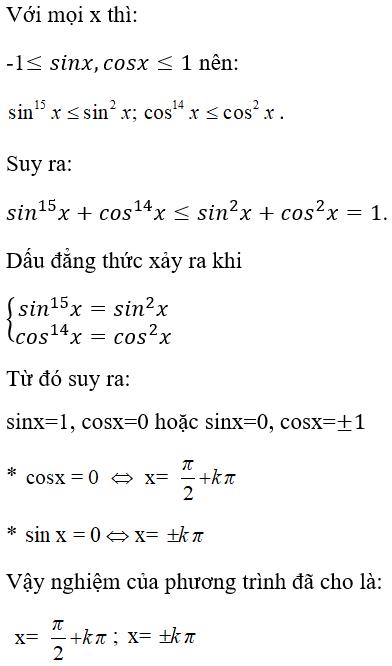
Chọn đáp án B
Câu 28: Có bao nhiêu giá trị nguyên của tham số m để phương trình sinxcosx – sinx – cosx + m = 0 có nghiệm?
A. 1
B. 2
C. 3
D. 4
Hiển thị đáp án

Chọn đáp án C
Câu 29: Cho x thỏa mãn 2sin2x – 3√6|sin x + cos x| + 8 = 0 . Tính sin2x
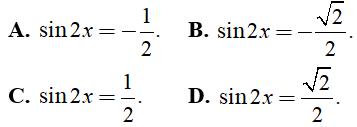
lần lượt là:
A. – 1/2 và 2 B. 1/2 và 2
C. -2 và -1/2 D. -2 và 1/2Hiển thị đáp án

Chọn đáp án C
Câu 30: Tìm giá trị lớn nhất M của hàm số 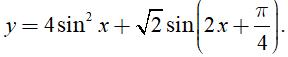
A. M = √2
B. M = √2 – 1
C. M = √2 + 1
D. M = √2 + 2
Hiển thị đáp án
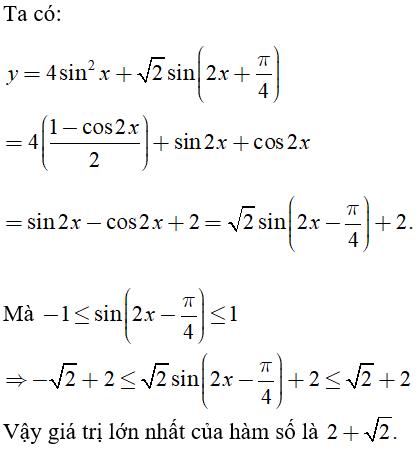
Chọn đáp án D
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây. Chúc các bạn lướt web vui vẻ !




