Đề thi học kì 1 môn Vật lí lớp 12 trường THPT chuyên Thái Nguyên năm 2020

I. PHẦN TRẮC NGHIỆM (6,0 Điểm): Học sinh tô phiếu TLTN

Câu 1 : Chọn câu đúng : Chu kì dao động của con lắc lò xo là :

        A. $T = \sqrt {\frac{{k\pi }}{m}}$

        B. $T = 2\pi \sqrt {\frac{k}{m}}$

        C. $T = \frac{\pi }{2}\sqrt {\frac{k}{m}}$

        D. $T = 2\pi \sqrt {\frac{m}{k}}$

Câu 2 : Dao động tắt dần:

     A. Có biên độ giảm dần theo thời gian

     B. Luôn có lợi                            

     C. Có biên độ không đổi theo thời gian

     D. Luôn có hại

Câu 3 : Dao động tổng hợp của hai dao động điều hòa cùng phương có phương trình dao động lần lượt là ${x_1} = 4\sqrt 2 \,{\rm{cos}}\left( {10\pi t + \frac{\pi }{3}} \right)cm,\,\,{x_2} = 4\sqrt 2 \,{\rm{cos}}\left( {10\pi t - \frac{\pi }{6}} \right)cm$ có phương trình là:

        A. $x = 8\,{\rm{cos}}\left( {10\pi t + \frac{\pi }{{12}}} \right)cm$

        B. $x = 4\sqrt 2 \,{\rm{cos}}\left( {10\pi t + \frac{\pi }{{12}}} \right)cm$

        C. $x = 8\,{\rm{cos}}\left( {10\pi t - \frac{\pi }{6}} \right)cm$

        D. $x = 4\sqrt 2 \,{\rm{cos}}\left( {10\pi t - \frac{\pi }{6}} \right)cm$

Câu 4 : Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số, biên độ ${A_1}$ và ${A_2}$ có biên độ $A$ thỏa mãn điều kiện nào là:

     A. $A = \left| {{A_1} - {A_2}} \right|$

     B. $A \le {A_1} + {A_2}$

     C. $A \ge \left| {{A_1} - {A_2}} \right|$

     D. $\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}$

Câu 5 : Sóng âm khi truyền trong chất rắn có thể là sóng dọc hoặc sóng ngang và lan truyền với tốc độ khác nhau. Tại trung tâm phòng chống thiên tai nhận được hai tín hiệu từ một vụ động đất cách nhau một khoảng thời gian $270s$. Hỏi tâm chấn động đất cách nơi nhận được tín hiệu bao xa? Biết tốc độ truyền sóng trong lòng đất với sóng ngang và sóng dọc lần lượt là $5\,km/s$ và $8\,\,km/s$.

        A. $570km$

        B. $3200km$

        C. $730km$

        D. $3600km$

Câu 6 : Khoảng cách giữa hai điểm gần nhất trên cùng một phương truyền sóng dao động cùng pha là:

     A. $\lambda /4$                        B. $\lambda$

     C. $2\lambda$                         D. $\lambda /2$

Câu 7 : Đơn vị cường độ âm là:

        A. $N/{m^2}$                        B. ${\rm{W}}/{m^2}$.

        C. ${\rm{W}}/m$                   D. $B\,\,(Ben)$

Câu 8 : Khi nói về dao động điều hòa, phát biểu nào sau đây là đúng?

A. Hợp lực tác dụng lên vật dao động điều hòa luôn hướng về vị trí cân bằng.                      

B. Dao động của con lắc lò xo luôn là dao động điều hòa.       

C. Dao động của con lắc đơn luôn là dao động điều hòa.        

D. Cơ năng của vật dao động điều hòa không phụ thuộc biên độ dao động.

Câu 9 : Một vật dao động điều hòa dọc theo trục $Ox$ với biên độ $20mm$, tần số $2Hz$. Tại thời điểm $t = 0s$ vật đi qua vị trí có li độ $1cm$ theo chiều âm. Phương trình dao động của vật là:

        A. $x = 2{\rm{cos}}\left( {4\pi t - \frac{\pi }{2}} \right)cm$

        B. $x = 2{\rm{cos}}\left( {4\pi t + \frac{\pi }{2}} \right)cm$

        C. $x = 1{\rm{cos}}\left( {4\pi t + \frac{\pi }{6}} \right)cm$

        D. $x = 1{\rm{cos}}\left( {4\pi t - \frac{\pi }{2}} \right)cm$

Câu 10 : Đặt điện áp $u = {U_o}\cos \omega t$ (${U_o}$ không đổi, $\omega$ thay đổi được) vào hai đầu đoạn mạch gồm điện trở $R$, cuộn cảm thuần có độ tự cảm $L$ và tụ điện có điện dung $C$ mắc nối tiếp. Tổng trở của mạch là

     A. $\sqrt {{R^2} + {{\left( {\omega L - \omega C} \right)}^2}}$

     B. $\sqrt {{R^2} + {{\left( {\frac{1}{{\omega L}} - \omega C} \right)}^2}}$

     C. $\sqrt {{R^2} + {{\left( {\omega L} \right)}^2} - {{\left( {\frac{1}{{\omega C}}} \right)}^2}}$

     D. $\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}}$

Câu 11 : Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại $A$ và $B$ dao động theo phương trình ${u_A} = {u_B} = a\cos 30\pi t$ ($a$ không đổi, $t$ tính bằng $s$). Tốc độ truyền sóng trong nước là $60cm/s$. Hai điểm $P,Q$ nằm tren mặt nước có hiệu khoảng cách đến hai nguồn là $PA - PB = 6cm,\,\,QA - QB = 12cm$. Kết luận về dao động của $P,Q$ là

        A. $P$ có biên độ cực tiểu, $Q$ có biên độ cực đại.

        B. $P,\,\,Q$ có biên độ cực tiểu.

       C. $P,\,\,Q$ có biên độ cực đại.

       D. $P$ có biên độ cực đại, $Q$ có biên độ cực tiểu.

Câu 12 : Trên một sợi dây đàn hồi dài $1m$, hai đầu cố định, đang có sóng dừng với $5$ nút sóng (kể cả hai đầu dây). Bước sóng của sóng truyền trên dây là:

     A. $2m$                                 B. $0,5m$

     C. $1,5m$                              D. $1m$

Câu 13 : Một vật dao động điều hòa với biên độ $A$ và chu kì $T$. Trong khoảng thời gian $\Delta t = 4T/3$, quãng đường lớn nhất $\left( {{S_{\max }}} \right)$ mà vật đi được là:

  A. $4A - A\sqrt 3$                 B. $A + A\sqrt 3$

  C. $4A + A\sqrt 3$                D. $2A\sqrt 3$ 

Câu 14 : Con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể. Hòn bi đang ở vị trí cân bằng thì được kéo xuống dưới theo phương thẳng đứng một đoạn $3cm$ rồi thả nhẹ cho nó dao động. Hòn bi thực hiện $50$ dao động mất $20s$. Cho $g = {\pi ^2} = 10m/{s^2}$. Tỉ số độ lớn lực đàn hồi cực đại và lực đàn hồi cực tiểu của lò xo $\left( {\frac{{{F_{dh\max }}}}{{{F_{dh\min }}}}} \right)$ khi dao động là:

     A. $7$                                            B. $0$

     C. $1/7$                                     D. $4$

Câu 15 : Trong bài thực hành đo gia tốc trọng trường của Trái Đất tại phòng thí nghiệm Vật lý Trường THPT Chuyên Tỉnh Thái Nguyên. Bạn Thảo Lớp Toán K29 đo chiều dài con lắc đơn có kết quả là $l = 100,00 \pm 1,00cm$ thì chu kì dao động $T = 2,00 \pm 0,01s$. Lấy ${\pi ^2} = 9,87$. Gia tốc trọng trường tại đó là:

        A. $g = 9,801 \pm 0,002m/{s^2}$

        B. $g = 9,801 \pm 0,0035m/{s^2}$ 

        C. $g = 9,87 \pm 0,20m/{s^2}$

        D. $g = 9,801 \pm 0,01m/{s^2}$

Câu 16 : Một chất điểm dao động điều hòa có vận tốc bằng không tại hai thời điểm liên tiếp ${t_1} = 2,2\,\left( s \right)$ và ${t_2} = 2,9\,\left( s \right)$. Tính từ thời điểm ban đầu (${t_o} = 0\,s$) đến thời điểm ${t_2}$ chất điểm đã đi qua vị trí cân bằng số lần là:

     A. $3$ lần                B. $4$ lần

     C. $6$ lần                D. $5$ lần

Câu 17 : Một đoạn mạch $AB$ gồm đoạn $AM$ và đoạn $MB$ mắc nối tiếp, đoạn $AM$ gồm cuộn dây có điện trở thuần, đoạn $MB$ chứa điện trở thuần và tụ điện mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ${u_{AB}} = {U_o}{\rm{cos}}\left( {\omega t + \varphi } \right)$ thì đồ thị biểu diễn sự phụ thuộc của điện áp hai đầu đoạn mạch $AM$ và $MB$ vào thời gian như hình vẽ. Lúc điện áp tức thời ${u_{AM}} =  - 75\sqrt 3 V$ và đang giảm thì tỉ số $\dfrac{{{u_{AM}}}}{{{U_o}}}$ gần nhất với giá trị nào sau đây?

 

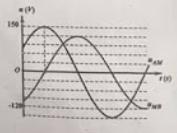
        A. $0,32$                         B. $- 0,48$

        C. $- 0,36$                      D. $0,65$

Câu 18 : Một vật có khối lượng ${m_1}$ treo vào một lò xo độ cứng $k$ thì chu kì dao động là ${T_1} = 3\,\,s$. Thay vật ${m_1}$ bằng vật ${m_2}$ thì chu kì dao động ${T_2} = 2\,\,s$. Thay vật ${m_2}$ bằng vật có khối lượng $\left( {2{m_1} + 4,5{m_2}} \right)$ thì chu kì dao động của con lắc là:

     A. $1/6\,\,s$                            B. $0,5s$

     C. $1/3\,\,s$                            D. $6s$

Câu 19 : Hai nguồn phát sóng kết hợp $A$ và $B$ trên mặt chất lỏng dao động theo phương trình : ${u_A} = {u_B} = A\cos \left( {100\pi t} \right)$. Tốc độ truyền sóng trên mặt chất lỏng $1m/s$. $I$ là trung điểm của $AB$. $M$ là điểm nằm trên đoạn $AI,\,\,N$ là điểm nằm trên đoạn $IB.$ Biết $IM = 5cm$ và $IN = 6,5cm$. Số điểm nằm trên đoạn $MN$ có biên độ cực đại cùng pha với $I$ là:

        A. $7$                                         B. $4$

        C. $5$                                         D. $6$

Câu 20 : Hai vật dao động điều  hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là ${x_1} = {A_1}\cos \left( {{\omega _1}t + {\varphi _1}\,} \right)\,\,(cm)$ và ${x_2} = {A_2}\cos \left( {{\omega _2}t + {\varphi _2}\,} \right)\,\,(cm)$. Biết $2{x_1}^2 + 3{x_2}^2 = 50\,\left( {c{m^2}} \right)$. Tại thời điểm ${t_1}$, vật thứ nhất đi qua vị trí có li độ ${x_1} = 1cm$ với vận tốc ${v_1} = 15cm/s$. Khi đó vật thứ hai có tốc độ bằng

     A. $8cm/s$                     B. $5cm/s$

     C. $2,5cm/s$                   D. $5\sqrt 3 cm/s$

II. PHẦN TỰ LUẬN (3,0 Điểm) : Học sinh làm bài trên giấy thi

Cho mạch điện $RLC$ mắc nối tiếp có biến trở .$R = 10\Omega ,\,\,L = \dfrac{{0,2}}{\pi }\left( H \right),\,\,C = \dfrac{{{{10}^{ - 5}}}}{\pi }\left( F \right)$.. Điện áp hai đầu mạch là $u = 60\sqrt 2 \,{\rm{cos}}\left( {10\pi t + \dfrac{\pi }{3}} \right)V$.

 

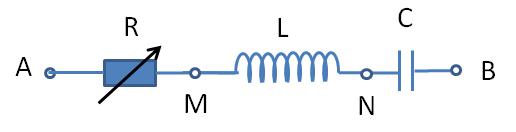
a) Tính tổng trở của cả mạch.

b) Viết biểu thức của cường độ dòng điện trong mạch $i$.

c) Viết biểu thức hiệu điện thế giữa hai đầu đoạn mạch $MB\,\,{u_{MB}}.$

d) Khi thay đổi độ lớn của điện trở người ta thấy ở giá trị ${R_1}$, công suất tỏa nhiệt cả điện trở $R$ đạt giá trị lớn nhất ${P_{Max}}$. Xây dựng biểu thức và tính giá trị ${R_1},{P_{Max}}$.

       

 

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN TIMDAPAN.COM

 

PHẦN I: TRẮC NGHIỆM

Câu 1 (NB):

Phương pháp:

Biểu thức tính chu kì dao động của con lắc lò xo 

Cách giải:

Chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\dfrac{m}{k}}$

Chọn D

Câu 2 (TH):

Phương pháp:

Sử dụng lí thuyết về dao động tắt dần

Cách giải:

A – đúng

B, D – sai vì: Dao động tắt dần vừa có lợi vừa có hại

C – sai vì: Dao động tắt dần có biên độ giảm dần theo thời gian

Chọn A

Câu 3 (VD):

Phương pháp:

+ Cách 1: Sử dụng công thức tổng hợp dao động điều hòa

– Biên độ dao động tổng hợp: .. 

– Pha dao động tổng hợp: $\tan \varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}}$

+ Cách 2: Sử dụng máy tính Casio:

$x = {A_1}\angle {\varphi _1} + {A_2}\angle {\varphi _2}$

Cách giải:

Ta có: $\left\{ \begin{array}{l}{x_1} = 4\sqrt 2 cos\left( {10\pi t + \dfrac{\pi }{3}} \right)cm\\{x_2} = 4\sqrt 2 cos\left( {10\pi t - \dfrac{\pi }{6}} \right)cm\end{array} \right.$. 

+ Cách 1:

– Biên độ dao động tổng hợp:

$\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}cos\left( {{\varphi _1} - {\varphi _2}} \right)\\ = {\left( {4\sqrt 2 } \right)^2} + {\left( {4\sqrt 2 } \right)^2} + 2.4\sqrt 2 .4\sqrt 2 .cos\left( {\dfrac{\pi }{3} - \left( { - \dfrac{\pi }{6}} \right)} \right)\\ = 64\\ \Rightarrow A = 8cm\end{array}$

– Pha ban đầu của dao động tổng hợp:

$\begin{array}{l}\tan \varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}} = \\ = \dfrac{{4\sqrt 2 \sin \dfrac{\pi }{3} + 4\sqrt 2 \sin  - \dfrac{\pi }{6}}}{{4\sqrt 2 cos\dfrac{\pi }{3} + 4\sqrt 2 cos - \dfrac{\pi }{6}}} = 2 - \sqrt 3 \\ \Rightarrow \varphi  = {15^0} = \dfrac{\pi }{{12}}\end{array}$

$\Rightarrow$ Phương trình dao động tổng hợp: $x = 8cos\left( {10\pi t + \dfrac{\pi }{{12}}} \right)cm$

+ Cách 2:

$\begin{array}{l}x = 4\sqrt 2 \angle \dfrac{\pi }{3} + 4\sqrt 2 \angle  - \dfrac{\pi }{6} = 8\angle \dfrac{\pi }{{12}}\\ \Rightarrow x = 8cos\left( {10\pi t + \dfrac{\pi }{{12}}} \right)cm\end{array}$.

Chọn A

Câu 4 (TH):

Phương pháp:

Sử dụng điều kiện của biên độ tổng hợp dao động điều hòa

Cách giải:

Ta có điều kiện của biên độ tổng hợp của hai dao động thành phần: $\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}$

Chọn D

Câu 5 (VD):

Phương pháp:

Sử dụng công thức: $s = v.t$

Cách giải:

Gọi:

– Khoảng cách từ tâm chấn động đến nơi nhận tín hiệu là $S$

– Thời gian nhận được tín hiệu thứ nhất (sóng ngang) là ${t_1}$

– Thời gian nhận được tín hiệu thứ 2 (sóng dọc) là ${t_2}$

Ta có:

+ Thời gian tín hiệu truyền đến trong lòng đất với sóng ngang là: ${t_1} = \dfrac{S}{{{v_1}}} = \dfrac{S}{5}$

+ Thời gian tín hiệu truyền đến trong lòng đất với sóng dọc là: ${t_2} = \dfrac{S}{{{v_2}}} = \dfrac{S}{8}$

Lại có:

$\begin{array}{l}{t_2} - {t_1} = 270s\\ \Leftrightarrow \dfrac{S}{5} - \dfrac{S}{8} = 270\\ \Rightarrow S = 3600km\end{array}$

Chọn D

Câu 6 (NB):

Phương pháp:

Sử dụng lí thuyết đại cương về sóng cơ học

Cách giải:

Khoảng cách giữa hai điểm gần nhất trên cùng một phương truyền sóng dao động cùng pha chính là một bước sóng $\lambda$.

Chọn B

Câu 7 (NB):

Phương pháp:

Sử dụng lí thuyết về cường độ âm: Cường độ âm I tại một điểm là đại lượng đo bằng năng lượng mà sóng âm tải qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian: $I = \dfrac{P}{S}$

Cách giải:

Ta có:  Cường độ âm I tại một điểm là đại lượng đo bằng năng lượng mà sóng âm tải qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền sóng trong một đơn vị thời gian:

$I = \dfrac{P}{S}$

Đơn vị: ${\rm{W}}/{m^2}$

Chọn B

Câu 8 (TH):

Phương pháp:

Sử dụng lí thuyết đại cương về dao động điều hòa.

Cách giải:

A – đúng.

B – sai vì dao động của con lắc lò xo có thể là dao động tắt dần, duy trì, cưỡng bức, …

C – sai vì dao động của con lắc đơn có thể là dao động tắt dần, duy trì, cưỡng bức, …

D – sai vì cơ năng của vật dao động điều hòa tỉ lệ thuận với bình phương biên độ dao động.

Chọn A

Câu 9 (VD):

Phương pháp:

+ Bước 1: Xác định biên độ

+ Bước 2: Xác định tần số góc, sử dụng biểu thức $\omega  = 2\pi f$

+ Bước 3: Xác định pha ban đầu .$t = 0:\left\{ \begin{array}{l}{x_0} = Acos\varphi \\v =  - A\omega \sin \varphi \end{array} \right.$. 

+ Bước 4: Viết phương trình dao động điều hòa

Cách giải:

Ta có:

+ Biên độ dao động của vật: $A = 20mm = 2cm$

+ Tần số góc của dao động: $\omega  = 2\pi f = 2\pi .2 = 4\pi \left( {rad/s} \right)$

+ Tại thời điểm ban đầu$t = 0$,

$\left\{ \begin{array}{l}{x_0} = Acos\varphi&nbsp; = 1cm\\v =&nbsp; - Asin\varphi&nbsp; < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}cos\varphi&nbsp; = \dfrac{1}{2}\\\sin \varphi&nbsp; > 0\end{array} \right. \Rightarrow \varphi&nbsp; = \dfrac{\pi }{3}$

+ Phương trình dao động của vật: $x = 2cos\left( {4\pi t + \dfrac{\pi }{3}} \right)cm$

Chọn B

Câu 10 (NB):

Phương pháp:

Sử dụng biểu thức tính tổng trở của mạch xoay chiều RLC mắc nối tiếp: $Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}$

Cách giải:

Ta có, tổng trở của mạch RLC mắc nối tiếp: $Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}$

Lại có: $\left\{ \begin{array}{l}{Z_L} = \omega L\\{Z_C} = \dfrac{1}{{\omega C}}\end{array} \right.$. 

$\Rightarrow Z = \sqrt {{R^2} + {{\left( {\omega L - \dfrac{1}{{\omega C}}} \right)}^2}}$

Chọn D

Câu 11 (VD):

Phương pháp:

+ Sử dụng biểu thức tính tần số: $f = \dfrac{\omega }{{2\pi }}$

+ Áp dụng biểu thức tính bước sóng: $\lambda&nbsp; = \dfrac{v}{f}$

+ Áp dụng điều kiện để có cực đại, cực tiểu:

– Cực đại: ${d_2} - {d_1} = k\lambda$

– Cực tiểu: ${d_2} - {d_1} = \left( {2k + 1} \right)\dfrac{\lambda }{2}$

Cách giải:

+ Tần số của sóng: $f = \dfrac{\omega }{{2\pi }} = \dfrac{{30\pi }}{{2\pi }} = 15Hz$

+ Bước sóng: $\lambda&nbsp; = \dfrac{v}{f} = \dfrac{{60}}{{15}} = 4cm$

+ Điểm P có:  $PA - PB = 6cm = \dfrac{3}{2}\lambda$

$\Rightarrow P$ thuộc cực tiểu số 2 tính từ trung trực AB đi ra

Điểm Q có: $QA - QB = 12cm = 3\lambda$

$\Rightarrow Q$ thuộc cực đại số 3 tính từ trung trực AB đi ra

Chọn A

Câu 12 (VD):

Phương pháp:

Vận dụng điều kiện sóng dừng trên dây 2 đầu cố định: $l = k\dfrac{\lambda }{2}$

k = số bụng

k+1 = số nút

Cách giải:

Ta có:

Sóng dừng trên dây 2 đầu cố định: $l = k\dfrac{\lambda }{2}$ (1)

Lại có 5 nút sóng $\Rightarrow k = 5 - 1 = 4$

Thay vào (1) ta được: $1 = 4\dfrac{\lambda }{2} \Rightarrow \lambda&nbsp; = 0,5m$

Chọn B

Câu 13 (VD):

Phương pháp:

Áp dụng biểu thức tính quãng đường lớn nhất vật đi được trong khoảng thời gian $\Delta t < \dfrac{T}{2}$ : ${S_{max}} = 2A\sin \dfrac{{\Delta \varphi }}{2}$

Cách giải:

 Ta có: $\Delta t = \dfrac{{4T}}{3} = T + \dfrac{T}{3}$

$\Rightarrow$ Quãng đường vật đi được: $S = {S_T} + {S_{\max \left( {\dfrac{T}{3}} \right)}}$

Ta có:

+ ${S_T} = 4A$

+ Quãng đường lớn nhất vật đi được trong khoảng thời gian $\dfrac{T}{3}$ : ${S_{max}} = 2A\sin \dfrac{{\Delta \varphi }}{2}$

Ta có: $\Delta \varphi&nbsp; = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{3} = \dfrac{{2\pi }}{3}$

$\Rightarrow {S_{\max }} = 2A\sin \dfrac{{\dfrac{{2\pi }}{3}}}{2} = \sqrt 3 A$

$\Rightarrow$ Quãng đường lướn nhất mà vật đi được trong khoảng thời gian $\Delta t = \dfrac{{4T}}{3}$ là: $S = 4A + \sqrt 3 A$ 

Chọn C

Câu 14 (VD):

Phương pháp:

+ Sử dụng biểu thức tính chu kì: $T = \dfrac{{\Delta t}}{N}$

+ Độ biến dạng của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k}$

+ Sử dụng biểu thức tính lực đàn hồi: ${F_{dh}} = k.$độ biến dạng của lò xo

Cách giải:

Ta có:

+ Biên độ dao động của vật: $A = 3cm$

+ Chu kì dao động của vật: $T = \dfrac{{20}}{{50}} = 0,4s$

+ Độ dãn của lò xo tại vị trí cân bằng: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{g{T^2}}}{{4{\pi ^2}}} = \dfrac{{10.0,{4^2}}}{{4.10}} = 0,04m = 4cm$

Lực đàn hồi cực đại tại vị trí thấp nhất: ${F_{dhMax}} = k\left( {\Delta l + A} \right)$  (1)

Nhận thấy $\Delta l > A$

$\Rightarrow {F_{dhMin}} = k\left( {\Delta l - A} \right)$ (2)

Từ (1) và (2), ta suy ra: $\dfrac{{{F_{dhMax}}}}{{{F_{dhMin}}}} = \dfrac{{k\left( {\Delta l + A} \right)}}{{k\left( {\Delta l - A} \right)}} = \dfrac{{\Delta l + A}}{{\Delta l - A}} = \dfrac{{4 + 3}}{{4 - 3}} = 7$

Chọn A

Câu 15 (VD):

Phương pháp:

+ Vận dụng biểu thức tính chu kì: $T = 2\pi \sqrt {\dfrac{l}{g}}$

+ Vận dụng biểu thức tính sai số

Cách giải:

Ta có chu kì $T = 2\pi \sqrt {\dfrac{l}{g}}$

$\Rightarrow$ Gia tốc rơi tự do: $g = \dfrac{{4{\pi ^2}l}}{{{T^2}}}$

+ Giá trị trung bình của gia tốc trọng trường: $\overline g&nbsp; = \dfrac{{4{\pi ^2}\overline l }}{{{{\overline T }^2}}} = \dfrac{{4{\pi ^2}.1}}{{{2^2}}} = 9,87m/{s^2}$

+ Sai số:

$\begin{array}{l}\dfrac{{\Delta g}}{{\overline g }} = \dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }}\\ \Rightarrow \Delta g = \left( {\dfrac{{\Delta l}}{{\overline l }} + 2\dfrac{{\Delta T}}{{\overline T }}} \right)\overline g \\ = \left( {\dfrac{1}{{100}} + 2\dfrac{{0,01}}{2}} \right)9,87\\ = 0,1974 \approx 0,2m/{s^2}\end{array}$

$\Rightarrow g = \overline g&nbsp; \pm \Delta g = 9,87 \pm 0,2{\rm{ m/}}{{\rm{s}}^2}$

Chọn C

Câu 16 (VD):

Phương pháp:

+ Vận có vận tốc bằng 0 khi ở vị trí biên

+ Sử dụng trục thời gian suy ra từ vòng tròn

 

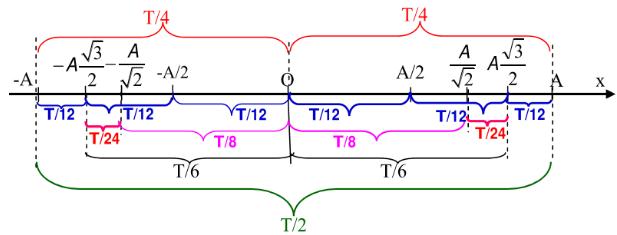
Cách giải:

+ Ta có, vật có vận tốc bằng 0 khi ở vị trí biên

+ Khoảng thời gian giữa 2 lần liên tiếp vật có vận tốc bằng 0 là $\dfrac{T}{2}$

$\begin{array}{l} \Rightarrow {t_2} - {t_1} = \dfrac{T}{2} \Leftrightarrow 2,9 - 2,2 = \dfrac{T}{2}\\ \Rightarrow T = 1,4s\end{array}$

+ Khoảng thời gian từ ${t_0} = 0s$ đến ${t_2} = 2,9s$ là $\Delta t = 2,9 - 0 = 2,9s = 2T + \dfrac{T}{{14}}$

Trong 1 chu kì vật qua VTCB 2 lần

$\Rightarrow$ Trong 2 chu kì vật qua VTCB 4 lần

Trong $\dfrac{T}{{14}}$ vật qua VTCB 0 lần

$\Rightarrow$ Trong khoảng thời gian từ ${t_0} = 0s$ đến ${t_2} = 2,9s$ vật qua VTCB 4 lần

Chọn B

Câu 17 (VD):

Phương pháp:

+ Đọc đồ thị

+ Áp dụng biểu thức tức thời: $u = {u_R} + {u_L} + {u_C}$

Cách giải:

Từ đồ thị, ta có: $\left\{ \begin{array}{l}{U_{0AM}} = 150V\\{U_{0MB}} = 120V\end{array} \right.$

${u_{AM}}$ nhanh pha hơn ${u_{MB}}$ một góc $\dfrac{\pi }{2}$

$\Rightarrow$ Điện áp cực đại giữa hai đầu đoạn mạch ${U_0} = \sqrt {U_{0AM}^2 + U_{0MB}^2}&nbsp; = \sqrt {{{150}^2} + {{120}^2}}&nbsp; = 30\sqrt {41} V$

+ Biểu diễn dao động điện tương ứng trên đường tròn, ta thấy khi ${u_{AM}} =&nbsp; - 75\sqrt 3 V = \dfrac{{ - {U_{0AM}}\sqrt 3 }}{2}$

 

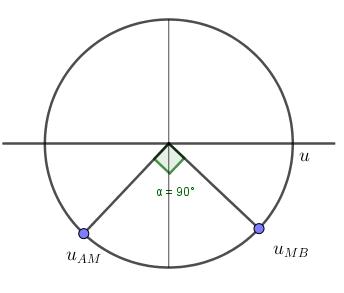
Thì ${u_{MB}} = \dfrac{{{U_{0MB}}}}{2} = \dfrac{{120}}{2} = 60V$

$\Rightarrow {u_{AB}} = {u_{AM}} + {u_{MB}} =&nbsp; - 75\sqrt 3&nbsp; + 60 \approx&nbsp; - 69,9V$

$\Rightarrow \dfrac{{{u_{AB}}}}{{{U_0}}} = \dfrac{{ - 69,9}}{{30\sqrt {41} }} =&nbsp; - 0,364$

Chọn C

Câu 18 (VD):

Phương pháp:

+ Vận dụng biểu thức tính chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt {\dfrac{m}{k}}$

+ Chu kì ${T^2} \sim m$

Cách giải:

Ta có, chu kì $T = 2\pi \sqrt {\dfrac{m}{k}}$

+ Khi vật có khối lượng ${m_1}$ thì ${T_1} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}}$

+ Khi vật có khối lượng ${m_2}$ thì ${T_2} = 2\pi \sqrt {\dfrac{{{m_2}}}{k}}$

Lại có ${T^2} \sim m$

 Khi thay bằng vât ${m_3} = 2{m_1} + 4,5{m_2}$ thì:

$\begin{array}{l}T_3^2 = 2T_1^2 + 4,5T_2^2\\ \Rightarrow {T_3} = \sqrt {2T_1^2 + 4,5T_2^2} \\ = \sqrt {{{2.3}^2} + 4,{{5.2}^2}}&nbsp; = 6s\end{array}$

Chọn D

Câu 19 (VD):

Phương pháp:

+ Vận dụng biểu thức tính bước sóng: $\lambda&nbsp; = \dfrac{v}{f}$

+ Sử dụng điều kiện dao động với biên độ cực đại: ${d_2} - {d_1} = k\lambda$

Cách giải:

Ta có,

+ Bước sóng của sóng: $\lambda&nbsp; = \dfrac{v}{f} = \dfrac{v}{{\dfrac{\omega }{{2\pi }}}} = \dfrac{1}{{\dfrac{{100\pi }}{{2\pi }}}} = 0,02m = 2cm$

+ Xét điểm C trên AB cách I: $IC = d$

Ta có phương trình sóng tại C: $\left\{ \begin{array}{l}{u_{AC}} = Acos\left( {100\pi t - \dfrac{{2\pi {d_1}}}{\lambda }} \right)\\{u_{BC}} = Acos\left( {100\pi t - \dfrac{{2\pi {d_2}}}{\lambda }} \right)\end{array} \right.$

C là điểm dao động với biên độ cực đại khi ${d_1} - {d_2} = k\lambda$

Ta có: ${d_1} - {d_2} = \left( {\dfrac{{AB}}{2} + d} \right) - \left( {\dfrac{{AB}}{2} - d} \right) = 2d = k\lambda$

$\Rightarrow d = k\dfrac{\lambda }{2} = k\dfrac{2}{2} = k\left( {cm} \right)$ với $k = 0, \pm 1, \pm 2,...$

Ta có:

$\begin{array}{l} - 5 \le d \le 6,5\\ \Leftrightarrow&nbsp; - 5 \le k \le 6,5\\ \Rightarrow k = 6, \pm 5, \pm 4, \pm 3, \pm 2, \pm 1,0\end{array}$ 

$\Rightarrow$ Có 12 giá trị của k

$\Rightarrow$ Trên MN có 12 điểm dao động với biên độ cực đại

Trung điểm I của AB là cực đại bậc 0 $\left( {k = 0} \right)$

Các điểm cực đại cùng pha với I cũng là chính là cùng pha với nguồn ứng với $k =&nbsp; - 4, - 2,2,4,6$

Vậy có 5 điểm dao động với biên độ cực đại và cùng pha với I

Chọn C

Câu 20 (VD):

Phương pháp:

+ Vận dụng phương pháp đạo hàm

+ $v = x'$

Cách giải:

Ta có: $2x_1^2 + 3x_2^2 = 50\left( {c{m^2}} \right)$  (1)

+ Khi $\left\{ \begin{array}{l}{x_1} = 1cm\\{v_1} = 15cm/s\end{array} \right.$ thay vào (1) ta được: ${2.1^2} + 3.x_2^2 = 50$

$\Rightarrow \left| {{x_2}} \right| = 4cm$

Đạo hàm 2 vế của (1) ta được:

$4{x_1}{x_1}' + 6{x_2}{x_2}' = 0$

$\Leftrightarrow 4{x_1}{v_1} + 6{x_2}{v_2} = 0$  (2)

Thay $\left\{ \begin{array}{l}{x_1} = 1cm\\{v_1} = 15cm/s\end{array} \right.$ và $\left| {{x_2}} \right| = 4cm$ vào (2) ta được $\left| {{v_2}} \right| = 2,5cm/s$

Chọn C

PHẦN II: TỰ LUẬN

Bài 1 (VD)

Phương pháp:

a) Sử dụng các biểu thức tính:

+ Cảm kháng: ${Z_L} = \omega L$

+ Dung kháng: ${Z_C} = \dfrac{1}{{\omega C}}$

+ Tổng trở: $Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}$

b) Sử dụng máy tính Casio: $i = \dfrac{u}{{\overline Z }} = \dfrac{{{U_0}\angle {\varphi _u}}}{{R + \left( {{Z_L} - {Z_C}} \right){\rm{i}}}}$

c) Sử dụng máy tính Casio: ${u_{MN}} = i.\overline {{Z_{MB}}}&nbsp; = {I_0}\angle {\varphi _i}.\left( {{Z_L} - {Z_C}} \right)i$

d) Sử dụng biểu thức tính công suất: $P = UIcos\varphi$

Cách giải:

 

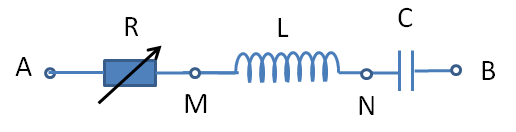
a) Ta có:

+ Điện trở $R = 10\Omega$

+ Cảm kháng: ${Z_L} = \omega L = 100\pi .\dfrac{{0,2}}{\pi } = 20\Omega$

+ Dung kháng: ${Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 3}}}}{\pi }}} = 10\Omega$

Tổng trở của mạch: $Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}&nbsp; = \sqrt {{{10}^2} + {{\left( {20 - 10} \right)}^2}}&nbsp; = 10\sqrt 2 \Omega$

b) Ta có:  $u = 60\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{3}} \right)V = 60\sqrt 2 \angle \dfrac{\pi }{3}$

Cường độ dòng điện: $i = \dfrac{u}{{\overline Z }} = \dfrac{{{U_0}\angle {\varphi _u}}}{{R + \left( {{Z_L} - {Z_C}} \right)i}} = \dfrac{{60\sqrt 2 \angle \dfrac{\pi }{3}}}{{10 + \left( {20 - 10} \right)i}} = 6\angle \dfrac{\pi }{{12}}$

$\Rightarrow$ Biểu thức cường độ dòng điện trong mạch: $i = 6cos\left( {100\pi t + \dfrac{\pi }{{12}}} \right)A$

c) ${u_{MN}} = i.\overline {{Z_{MB}}}&nbsp; = {I_0}\angle {\varphi _i}.\left( {{Z_L} - {Z_C}} \right)i = 6\angle \dfrac{\pi }{{12}}.\left( {20 - 10} \right)i = 60\angle \dfrac{{7\pi }}{{12}}$

$\Rightarrow {u_{MB}} = 60cos\left( {100\pi t + \dfrac{{7\pi }}{{12}}} \right)$

d)

Ta có, công suất tỏa nhiệt trên điện trở 

$P = UIc{\rm{os}}\varphi {\rm{ = }}{{\rm{I}}^2}R = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \dfrac{{{U^2}}}{{R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}$

Để Pmax $\to {\left[ {R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right]_{\min }}$

Ta có: $R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R\dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}&nbsp; = 2\left| {{Z_L} - {Z_C}} \right|$

Dấu “=” xảy ra $\leftrightarrow {R^2} = {({Z_L} - {Z_C})^2} \to R = \left| {{Z_L} - {Z_C}} \right| = 20 - 10 = 10\Omega$

${P_{Max}} = \dfrac{{{U^2}}}{{2R}} = \dfrac{{{{60}^2}}}{{2.10}} = 180W$