Hướng dẫn giải chi tiết Đề kiểm tra học kì 1 môn Toán lớp 11 có đáp án đề số 6 có đáp án nhanh và chính xác nhất dành cho học sinh tham khảo được tổng hợp bởi Giải bài tập. Mời các bạn học sinh cùng tham khảo.
Đề bài
A. PHẦN TRẮC NGHIỆM: (6 điểm)
Câu 1 : Giải phương trình lượng giác 4sin4x+12cos2x−7=0 có nghiệm:
A. x=π4+kπ,(k∈Z).
B. x=−π4+kπ,(k∈Z).
C. x=±π4+k2π,(k∈Z).
D. x=π4+kπ2,(k∈Z).
Câu 2 : Cho hai đường thẳng d1 và d2 chéo nhau. Có bao nhiêu mặt phẳng chứa d1và song song với d2?
A. 2. B. 4.
C. 3. D. 1.
Câu 3 : Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M, N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:
A. (ABD).
B. (CMN).
C. (BCD).
D. (ACD).
Câu 4 : Nghiệm của phương trình sau 3–√sinx−cosx=2 .
A. x=π3+kπ,(k∈Z).
B. x=2π3+k2π,(k∈Z).
C. x=π2+k2π,(k∈Z).
D. x=π3+k2π,(k∈Z).
Câu 5 : Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho ?
A. 4 B. 3.
C. 2. D. 6.
Câu 6 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, Nlần lượt là trung điểm AD và BC.Giao tuyến của hai mặt phẳng (SMN) và (SAC) là:
A. SO, O là tâm hình bình hành ABCD.
B. SD
C. SG, G là trung điểm AB.
D. SF, F là trung điểm CD.
Câu 7 : Cho dãy số (un)xác định bởi:{u1=1un=2un−1+3∀n≥2.Viết năm số hạng đầu của dãy;
A. 1;5;17;29;61.
B. 1;5;14;29;61.
C. 1;5;13;28;61..
D. 1;5;13;29;61
Câu 8 : Cho các chữ số 2, 3, 4, 5, 6, 7. Khi đó có bao nhiêu số tự nhiên có ba chữ số được thành lập từ các chữ số đã cho?
A. 216. B. 120.
C. 18. D. 720.
Câu 9 : Công thức tính Ckn là
A. n!.
B. n!(n−k)!.
C. n!k!(n−k)!.
D. n!k!.
Câu 10 : Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

A. 24. B. 9.
C. 18. D. 10.
Câu 11 : Cho hình bình hành ABEF. Gọi D, C lần lượt là trung điểm của AF và BE, O là giao điểm của AC và BD, I là giao điểm của FC và DE. Phép tịnh tiến TFI−→ biến tam giác DIF thành tam giác nào sau đây:
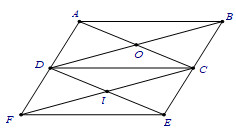
A. ΔAOD.
B. ΔCIE.
C. ΔOBC.
D. ΔOCI.
Câu 12 : Đề kiểm tra hoc kì 1 môn Toán khối 11 ở một Trường THPT gồm 2 phần tự luận và trắc nghiệm, trong đó phần tự luận có 13 đề, phần trắc nghiệm có 10 đề. Mỗi học sinh phải làm bài thi gồm một đề tự luận và một đề trắc nghiệm. Hỏi Trường THPT đó có bao nhiêu cách chọn đề thi?
A. 130. B. 23.
C. 253. D. 506.
Câu 13 : Hàm số nào sau đây là hàm số lẻ ?
A. y=cos3x.
B. y=sinx+cos3x.
C. y=sinx+tan3x.
D. y=tan2x.
Câu 14 : Gieo ngẫu nhiên một con xúc sắc cân đối và đồng chất 3 lần. Khi đó n(Ω)=?
A. 6.5.4.
B. 36.
C. 6.6.6.
D. 6.6.5.
Câu 15 : Nghiệm của phương trình cos2x+3–√sin2x=1+sin2x là:
A. ⎡⎣⎢⎢x=k23πx=π3+k23π.
B. [x=kπx=π3+kπ.
C. ⎡⎣⎢⎢x=k12πx=π3+k12π.
D. [x=k2πx=π3+k2π.
Câu 16 : Hệ số của x7 trong khai triển của (3−x)9
A. −9C79. B. −C79.
C. 9C79. D. C79.
Câu 17 : Tập xác định của hàm số y=22−sinx−−−−−−−√:
A. (2;+∞).
B. R∖{2}.
C. R
D. [2;+∞).
Câu 18 : Xếp 7 người vào một băng ghế có 9 chỗ. Hỏi có bao nhiêu cách xếp?
A. 36.
B. 2250.
C. 5040.
D. 181440.
Câu 19 : Cho hình bình hành ABCD. Phép tịnh tiến TDA−→− biến:
A. B thành C
B. C thành B
C. C thành A.
D. A thành D.
Câu 20 : Nghiệm của phương trình lượng giác: 2sin2x−3sinx+1=0 thỏa điều kiện 0<x<π2 là:
A.
B.
C.
D.
Câu 21 : Hàm số xác định khi:
A. .
B. .
C. .
D. .
Câu 22 : Có bao nhiêu mặt phẳng đi qua 3 điểm không thẳng hàng ?
A. B.
C. D.
Câu 23 : Điều kiện có nghiệm của pt là
A. .
B. .
C. .
D. .
Câu 24 : Trong mặt phẳng cho tứ giác , điểm . Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm ?
A. . B. .
C. D. .
Câu 25 : Cho 6 chữ số 2, 3, 4, 5, 6, 7. Có bao nhiêu số tự nhiên chẵn có 3 chữ số lập từ 6 chữ số đó.
A. 256. B. 108.
C. 36. D. 18.
Câu 26 : Một túi chứa 6 bi xanh, 4 bi đỏ. Lấy ngẫu nhiên 2 bi. Tính xác suất để được cả hai bi đều màu đỏ.
A.
B. .
C. .
D. .
Câu 27 : Nghiệm của phương trình là:
A. .
B. .
C. .
D. .
Câu 28: Cho tứ diện ABCD. G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm trên đoạn AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
A. A, J, M thẳng hàng.
B. J là trung điểm AM.
C. .
D.
Câu 29 : Nghiệm của phương trình là
A.
B.
C.
D.
Câu 30 : Cho hình chóp có Giao tuyến của mặt phẳng và mặt phẳng là đường thẳng
A. B.
C. D.
B. PHẦN TỰ LUẬN: (4 điểm)
Bài 1. (2.0 điểm). Giải các phương trình sau:
a)
b)
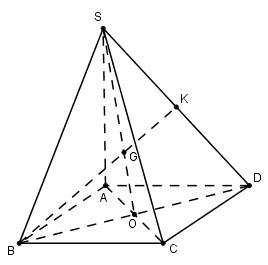
Bài 2 . (2.0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.
a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).
b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.
Lời giải chi tiết
A. PHẦN TRẮC NGHIỆM
|
1. D |
2. D |
3. D |
4. B |
5. A |
|
6. A |
7. D |
8. A |
9. C |
10. A |
|
11. D |
12. A |
13. C |
14. C |
15. B |
|
16. A |
17. C |
18. D |
19. B |
20. C |
|
21. A |
22. A |
23. B |
24. C |
25. B |
|
26. B |
27. D |
28. B |
29. C |
30. A |
B. PHẦN TỰ LUẬN
Bài 1:
Bài 2:
a) Gọi
(1)
Mà (2)
Từ (1) và (2) .
b) Trong mặt phẳng gọi
.
Ta có , mà BK và SO là các đường trung tuyến của tam giác SBD là trọng tâm tam giác SBD.
>
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Hy vọng bài viết trên sẽ hữu ích và tác động tích cực tới kết quả học tập của bạn. Mời bạn tham khảo thêm các tài liệu học tốt khác tại đây .




