Đề kiểm tra học kì 1 môn Toán lớp 11 có đáp án đề số 5

Đề bài

PHẦN I: TRẮC NGHIỆM (5,0 điểm – thời gian làm: 45 phút)

Câu 1 : Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 3\sin \,x + 4\cos x + 1$. Khẳng định nào sau đây đúng?

A. $M = 5,m =  - 5$.

B. $M = 8,m =  - 6$.

C. $M = 6,m =  - 2$.

D. $M = 6,m =  - 4$.

Câu 2 : Cho hình chóp S.ABCD biết AC cắt BD tại M, AB cắt CD tại N. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

A. SB.                          B. SM.

C. SC.                         D. SN.

Câu 3 : Tìm tập xác định của hàm số $y = \cot x$.

A. $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}$.

B. $R{\rm{\backslash }}\left\{ {k\pi ,k \in Z} \right\}$.

C. $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k2\pi ,k \in Z} \right\}$.

D. $R{\rm{\backslash }}\left\{ {k2\pi ,k \in Z} \right\}$.

Câu 4 : Cho đường tròn $\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 49$. Viết phương trình đường tròn $\left( {C'} \right)$ là ảnh của $\left( C \right)$ qua phép đối xứng trục $Oy$.

A. ${\left( {x - 1} \right)^2} + {\left( {y + 4} \right)^2} = 49$.

B. ${\left( {x - 4} \right)^2} + {\left( {y + 1} \right)^2} = 49$.        

C. ${\left( {x + 1} \right)^2} + {\left( {y + 4} \right)^2} = 49$.

D. ${\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} = 49$.

Câu 5 : Trong mặt phẳng Oxy cho 2 điểm $M\left( { - 3;2} \right)$,$M'\left( {3; - 2} \right)$. M’ là ảnh của M qua phép biến hình nào sau đây?

A. Phép đối xứng qua trục tung.

B. Phép đối xứng qua trục hoành.     

C. Phép đối xứng qua đường thẳng $y = x$.

D. Phép đối xứng qua tâm O.

Câu 6 : Một hộp có 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi từ hộp trên. Tính xác suất để được hai viên bi xanh?

A. $\dfrac{4}{7}$.                             B. $\dfrac{3}{7}$.

C. $\dfrac{1}{7}$.                             D. $\dfrac{2}{7}$.    

Câu 7 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Mặt phẳng qua MN cắt AD, BC lần lượt tại P, Q. Biết $MP$ cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?

A. I, C, D.

B. I, A, C.

C. I, B, D.

D. I, A, B.

Câu 8 : Tìm số hạng không chứa x trong khai triển ${\left( {x - \dfrac{2}{x}} \right)^8}$.

A. -70.                         B. -1120.

C. 70.                          D. 1120.

Câu 9 : Trong các hàm số sau, hàm số nào nghịch biến trên $\left( {0;\dfrac{\pi }{2}} \right)$?

A.$y = \cos x$.          

B. $y = \tan x$.

C. $y = \sin x$.

D. $y =  - \cos x$.

Câu 10 : Gọi ${x_0}$ là nghiệm dương nhỏ nhất của phương trình $2{\sin ^2}x + \sin x - 1 = 0$. Mệnh đề nào sau đây đúng?

A. ${x_0} \in \left[ {\dfrac{{5\pi }}{6};\dfrac{{3\pi }}{2}} \right]$.

B. ${x_0} \in \left( {\dfrac{\pi }{6};\dfrac{{5\pi }}{6}} \right)$.

C. ${x_0} \in \left( {0;\dfrac{\pi }{4}} \right)$.

D. ${x_0} \in \left( {\dfrac{\pi }{2};\pi } \right)$.

Câu 11 : Giải phương trình $\cos x =  - \dfrac{{\sqrt 2 }}{2}$.

A. $\left\{ {\dfrac{{3\pi }}{4} + k2\pi ,k \in Z} \right\}$.

B. $\left\{ { - \dfrac{\pi }{4} + k2\pi ;\dfrac{{5\pi }}{4} + k2\pi ,k \in Z} \right\}$.

C. $\left\{ { \pm \dfrac{{3\pi }}{4} + k2\pi ,k \in Z} \right\}$.

D. $\left\{ { \pm \dfrac{\pi }{4} + k2\pi ,k \in Z} \right\}$.

Câu 12 : Trên giá sách có 6 quyển sách tiếng Việt khác nhau, 4 quyển sách tiếng Anh khác nhau, 7 quyển sách tiếng Pháp khác nhau. Hỏi có bao nhiêu cách lấy từ giá trên 3 quyển sách sao cho có đủ cả sách tiếng Việt, tiếng Anh và tiếng Pháp?

A. 59.                          B. 17.

C. 680.                         D. 168.

Câu 13 : Trong mặt phẳng có 10 điểm phân biệt. Có bao nhiêu vectơ (khác vectơ – không) có điểm đầu và điểm cuối thuộc tập điểm đã cho?

A. 90.                          B. 45.

C. 5.                            D. 100.

Câu 14 : Tìm tập xác định của hàm số $y = \sqrt {\sin x - 1}$.

A. $\left\{ {\dfrac{\pi }{2} + k2\pi ,k \in Z} \right\}$.          

B. $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k2\pi ,k \in Z} \right\}$.

C. $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}$.

D. $\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}$.

Câu 15 : Cho hàm số $y = \tan \,x$. Khẳng định nào sau đây sai?

A. Hàm số là hàm số chẵn.    

B. Hàm số tuần hoàn với chu kì $\pi$.

C. Hàm số đồng biến trên mỗi khoảng $\left( { - \dfrac{\pi }{2} + k\pi ;\dfrac{\pi }{2} + k\pi } \right),\,\,k \in Z$. 

D. Tập xác định của hàm số là $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}$.

Câu 16 : Có bao nhiêu cách xếp khác nhau cho 5 bạn nam và 4 bạn nữ đứng thành một hàng ngang sao cho các bạn nữ đứng cạnh nhau?

A. 14400.

B. 5760.

C. 2880.

D. 17280.

Câu 17 : Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = \sin 2x$ trên $\left[ { - \dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$. Tìm $T = M + m$.

A. $T = 1 - \dfrac{{\sqrt 3 }}{2}$.   

B. $T = 1 + \dfrac{{\sqrt 3 }}{2}$.   

C. $T = \dfrac{1}{2}$.

D. $T = 0$.

Câu 18 : Cho đa thức $P\left( x \right) = {\left( {2x - 1} \right)^{1000}}$. Khai triển và rút gọn ta được đa thức $P\left( x \right) = {a_{1000}}{x^{1000}} + {a_{999}}{x^{999}} + ... + {a_1}x + {a_0}$. Đẳng thức nào sau đây đúng?

A. ${a_{1000}} + {a_{999}} + ... + {a_1} + {a_0} = 0$.

B. ${a_{1000}} + {a_{999}} + ... + {a_1} + {a_0} = {2^{1000}} - 1$.

C. ${a_{1000}} + {a_{999}} + ... + {a_1} + {a_0} = 1$.

D. ${a_{1000}} + {a_{999}} + ... + {a_1} + {a_0} = {2^{1000}}$.

Câu 19 : Cho tam giác ABC với trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O. Phép vị tự ${V_{\left( {G;k} \right)}}$ biến O thành H. Tìm k?

A. -2.                           B. $- \dfrac{1}{2}$.

C. $\dfrac{1}{2}$.                             D. 2.

Câu 20 : Cho hình đa giác đều H có 24 đỉnh, chọn ngẫu nhiên 4 đỉnh của hình H. Tính xác suất để 4 đỉnh chọn được tạo thành hình vuông?

A. $\dfrac{{120}}{{1771}}$.

B. $\dfrac{2}{{1771}}$.

C. $\dfrac{1}{{161}}$.

D. $\dfrac{1}{{1771}}$.

Câu 21 : Trong các mệnh đề sau, mệnh đề nào sai?

A. Phép dời hình là một phép đồng dạng.

B. Phép đồng dạng là một phép dời hình.                 

C. Có phép vị tự không phải phép dời hình. 

D. Phép vị tự là một phép đồng dạng.

Câu 22 : Cho hình bình hành ABCD, biết A, B cố định, điểm C di động trên đường thẳng $\Delta$ cố định. Khẳng định nào sau đây đúng?

A. Điểm D di động trên đường thẳng $\Delta '$ là ảnh của $\Delta$ qua phép đối xứng trục $AB$.

B. Điểm D di động trên đường thẳng $\Delta '$ là ảnh của $\Delta$ qua phép tịnh tiến theo $\overrightarrow {BA}$.

C. Điểm D di động trên đường thẳng $\Delta '$ là ảnh của $\Delta$ qua phép đối xứng tâm I (I là trung điểm của AB).                

D. Điểm D di động trên đường thẳng $\Delta '$ là ảnh của $\Delta$ qua phép tịnh tiến theo $\overrightarrow {AB}$.

Câu 23 : Phương trình $\sqrt 3 \sin 2x - 2{\cos ^2}x = 0$ có tập nghiệm được biểu diễn bởi bao nhiêu điểm trên đường tròn lượng giác?

A. 3.                            B. 2.

C. 6.                            D. 4.

Câu 24 : Tìm số nghiệm của phương trình $\tan 4x - \tan 2x - 4\tan \,x = 4\tan 4x.\tan 2x.\tan \,x$ thuộc đoạn $\left[ { - \pi ;\pi } \right]$.

A. 6.                            B. 7.

C. 2.                            D. 3.

Câu 25 : Cho $n \in N$ thỏa mãn $C_n^7 = 120$. Tính $A_n^7$.

A. 604800.                  B. 720.           

C. 120.                         D. 840.

PHẦN II: TỰ LUẬN (5,0 điểm – thời gian làm: 45 phút)

Câu 1 (1,5 điểm). Giải các phương trình sau:

a) $\cos 2x - 5\sin x - 3 = 0$.

b) $\left[ {1 + \cos \left( {x + \dfrac{\pi }{2}} \right)} \right]{\tan ^2}x - \cos x = 1$.

Câu 2 (1 điểm). Trong tuần lễ cấp cao Apec diễn ra từ ngày 06 đến ngày 11 tháng 11 năm 2017 tại Đà Nẵng, có 21 nên kinh tế thành viên tham dự, trong đó có 12 nền kinh tế sáng lập Apec. Tại một cuộc họp báo, mỗi nền kinh tế thành viên cử một đại diện tham gia. Một phóng viên đã chọn ngẫu nhiên 5 đại diện để phỏng vấn. Tính xác suất để 5 đại diện đó có cả đại diện của nền kinh tế thành viên sáng lập Apec và nền kinh tế thành viên không sáng lập Apec.

Câu 3 (1 điểm). Trong mặt phẳng tọa độ Oxy, cho đường thẳng $\Delta :2x - 3y + 7 = 0$. Phép tịnh tiến theo vectơ $\overrightarrow u \left( {5; - 3} \right)$ biến đường thẳng $\Delta$ thành đường thẳng $\Delta '$. Viết phương trình đường thẳng $\Delta '$.

Câu 4 (1,5 điểm).  Cho hình chóp tam giác S.ABC có G là trọng tâm tam giác ABC. Gọi A’, B’ lần lượt là trung điểm của SA, SB; điểm C’ nằm giữa hai điểm S và C.

a) Tìm giao điểm G’ của đường thẳng SG với mặt phẳng (A’B’C’).

b) Chứng minh rằng biểu thức $\dfrac{{3SG}}{{SG'}} - \dfrac{{SC}}{{SC'}}$ có giá trị không đổi.

Lời giải chi tiết

PHẦN I: TRẮC NGHIỆM (5,0 điểm – thời gian làm: 45 phút)

1. D	2. B	3. B	4. D	5. D
6. C	7. C	8. D	9. B	10. C
11. C	12. D	13. A	14. A	15. A
16. D	17. A	18. C	19. A	20. D
21. B	22. B	23. D	24. B	25. A

PHẦN II: TỰ LUẬN (5,0 điểm – thời gian làm: 45 phút)

Câu 1:

a) $\cos 2x - 5\sin x - 3 = 0$

$\Leftrightarrow 1 - 2{\sin ^2}x - 5\sin x - 3 = 0$

$\Leftrightarrow - 2{\sin ^2}x - 5\sin x - 2 = 0$

$\Leftrightarrow \left[ \matrix{ \sin x = - {1 \over 2} \hfill \cr \sin \,x = - 2\,\,\text{(vô nghiệm)} \hfill \cr} \right.$

$\Leftrightarrow \sin x = - {1 \over 2}$

$\Leftrightarrow \left[ \matrix{ x = - {\pi \over 6} + k2\pi \hfill \cr x = \pi - \left( { - {\pi \over 6}} \right) + k2\pi \hfill \cr} \right.,k \in Z$

$\Leftrightarrow \left[ \matrix{ x = - {\pi \over 6} + k2\pi \hfill \cr x = {{7\pi } \over 6} + k2\pi \hfill \cr} \right.,k \in Z$

Vậy, phương trình có tập nghiệm $\left\{ { - {\pi  \over 6} + k2\pi ;{{7\pi } \over 6} + k2\pi ,k \in Z} \right\}$

b) $\left[ {1 + \cos \left( {x + {\pi  \over 2}} \right)} \right]{\tan ^2}x - \cos x = 1$ (*)

ĐKXĐ: $\cos x \ne 0$

Phương trình $(*) \Leftrightarrow \left( {1 - \sin \,x} \right).{{{{\sin }^2}x} \over {{{\cos }^2}x}} - \cos x - 1 = 0$

$\eqalign{ & \Leftrightarrow \left( {1 - \sin \,x} \right).{{1 - {{\cos }^2}x} \over {1 - {{\sin }^2}x}} - \cos x - 1 = 0 \cr & \Leftrightarrow \left( {1 - \sin \,x} \right).{{\left( {1 - \cos x} \right)\left( {1 + \cos x} \right)} \over {\left( {1 - \sin x} \right)\left( {1 + \sin x} \right)}} - \cos x - 1 = 0 \cr & \Leftrightarrow {{\left( {1 - \cos x} \right)\left( {1 + \cos x} \right)} \over {1 + \sin x}} - \cos x - 1 = 0 \cr & \Leftrightarrow \left( {1 - \cos x} \right)\left( {1 + \cos x} \right) - \left( {1 + \cos x} \right)\left( {1 + \sin x} \right) = 0 \cr & \Leftrightarrow \left( {1 + \cos x} \right)\left( {\left( {1 - \cos x} \right) - \left( {1 + \sin x} \right)} \right) = 0 \cr & \Leftrightarrow \left( {1 + \cos x} \right)\left( { - \cos x - \sin \,x} \right) = 0\cr& \Leftrightarrow \left[ \matrix{ \cos x = - 1 \hfill \cr \sin \,x = - \cos x \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ \cos x = - 1 \hfill \cr \tan \,x = - 1 \hfill \cr} \right. \cr&\Leftrightarrow \left[ \matrix{ x = \pi + k2\pi \hfill \cr x = - {\pi \over 4} + k\pi \hfill \cr} \right.,\,k \in Z \cr}$

Vậy, phương trình có tập nghiệm $\left\{ {\pi  + k2\pi ; - {\pi  \over 4} + k\pi ,k \in Z} \right\}$

Câu 2: (1 điểm).

Số phần tử của không gian mẫu: $n\left( \Omega  \right) = C_{21}^5$

A: “5 đại diện đó có cả đại diện của nền kinh tế thành viên sáng lập Apec và nền kinh tế thành viên không sáng lập Apec”

$\Rightarrow \overline A$: “5 đại diện đó chỉ có đại diện của nền kinh tế thành viên sáng lập Apec hoặc chỉ có nền kinh tế thành viên không sáng lập Apec”

$\eqalign{ & n\left( {\overline A } \right) = C_{12}^5 + C_{21 - 12}^5 = C_{12}^5 + C_9^5 = 792 + 126 = 918 \cr & \Rightarrow P\left( {\overline A } \right) = {{n\left( {\overline A } \right)} \over {n\left( \Omega \right)}} = {{C_{12}^5 + C_9^5} \over {C_{21}^5}} = {{918} \over {20349}} = {6 \over {133}} \cr & \Rightarrow P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - {6 \over {133}} = {{127} \over {133}} \cr}$

Câu 3: (1 điểm).

${T_{\overrightarrow u \left( {5; - 3} \right)}}:M\left( {x;y} \right) \mapsto M'\left( {x';y'} \right)\,\,$

$\Leftrightarrow \left\{ \matrix{ x' = x + 5 \hfill \cr y' = y - 3 \hfill \cr} \right.$

$M\left( {x;y} \right) \in \Delta  \Rightarrow M'\left( {x';y'} \right) \in \Delta '$

$\left\{ \matrix{ x' = x + 5 \hfill \cr y' = y - 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = x' - 5 \hfill \cr y = y' + 3 \hfill \cr} \right.$

Khi đó: $2\left( {x' - 5} \right) - 3\left( {y' + 3} \right) + 7 = 0$

$\Leftrightarrow 2x' - 3y' - 12 = 0$

Phương trình đường thẳng $\Delta '$ là: $2x - 3y - 12 = 0$

Câu 4:

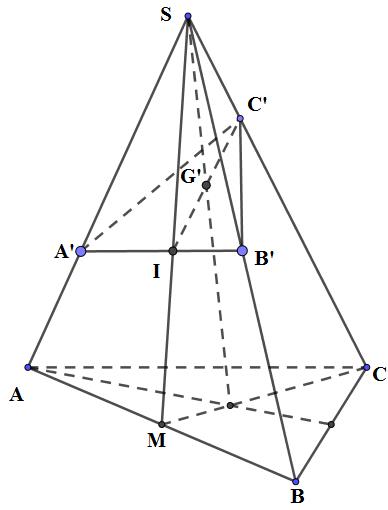
a) 

a) Gọi M là trung điểm của AB, do G là trọng tâm tam giác ABC

 M, G, C thẳng hàng

Trong (SAB), gọi I là giao điểm của SM và A’B’

Trong (SMC), gọi G’ là giao điểm của IC’ và SG

Khi đó: 

$\left\{ \matrix{ G' \in SG \hfill \cr G' \in IC' \subset \left( {A'B'C'} \right) \hfill \cr} \right. \Rightarrow G' = SG \cap \left( {A'B'C'} \right)$

b)* Ta chứng minh:  ${{3SG} \over {SG'}} = {{SA} \over {SA'}} + {{SB} \over {SB'}} + {{SC} \over {SC'}}$ với A’, B’, C’ là 3 điểm bất kì lần lượt nằm trên các đoạn SA, SB, SC (khác S):

G là trọng tâm tam giác ABC 

 

$\Rightarrow {S_{\Delta ABG}} = {S_{\Delta BCG}} = {S_{\Delta ACG}}$

$\Rightarrow {V_{S.ABG}} = {V_{S.ACG}} = {V_{S.BCG}}$

$\Rightarrow {V_{S.ABG}} = {V_{S.ACG}} = {V_{S.BCG}} = {{{V_{S.ABC}}} \over 3}$

Đặt: ${V_{S.ABC}} = V;\,\,\,{V_{S.ABG}} = {V_{S.ACG}} = {V_{S.BCG}} = {V_0}\,\,$$\Rightarrow V = 3{V_0}$

Gọi thể tích khối chóp S.A’B’C’ là $V'$ $\Rightarrow V' = {V_{S.A'B'G'}} + {V_{S.A'C'G'}} + {V_{S.B'C'G'}}$

$\Rightarrow \dfrac{{V'}}{{{V_0}}} = \dfrac{{{V_{S.A'B'G'}}}}{{{V_0}}} + \dfrac{{{V_{S.A'C'G'}}}}{{{V_0}}} + \dfrac{{{V_{S.B'C'G'}}}}{{{V_0}}}$

$\eqalign{ & \Leftrightarrow {{V'} \over {{1 \over 3}V}} = {{SA'.SB'.SG'} \over {SA.SB.SG}} + {{SC'.SB'.SG'} \over {SC.SB.SG}} + {{SA'.SC'.SG'} \over {SA.SC.SG}} \cr & \Leftrightarrow 3.{{SA'.SB'.SC'} \over {SA.SB.SC}} = {{SG'} \over {SG}}\left( {{{SA'.SB'} \over {SA.SB}} + {{SC'.SB'} \over {SC.SB}} + {{SA'.SC'} \over {SA.SC}}} \right) \cr & \Leftrightarrow 3.{{SA'.SB'.SC'} \over {SA.SB.SC}} = {{SG'} \over {SG}}.{{SA'.SB'.SC + SC'.SB'.SA + SA'.SC'.SB} \over {SA.SB.SC}} \cr & \Leftrightarrow 3SA'.SB'.SC' = {{SG'} \over {SG}}.\left( {SA'.SB'.SC + SC'.SB'.SA + SA'.SC'.SB} \right) \cr & \Leftrightarrow {{3SG} \over {SG'}} = {{SA'.SB'.SC + SC'.SB'.SA + SA'.SC'.SB} \over {SA'.SB'.SC'}} \cr & \Leftrightarrow {{3SG} \over {SG'}} = {{SA} \over {SA'}} + {{SB} \over {SB'}} + {{SC} \over {SC'}}\,\,(dpcm) \cr}$

Chứng minh: ${{3SG} \over {SG'}} - {{SC} \over {SC'}}$ có giá trị không đổi:

Ta có: ${{3SG} \over {SG'}} = {{SA} \over {SA'}} + {{SB} \over {SB'}} + {{SC} \over {SC'}}$

$\Leftrightarrow {{3SG} \over {SG'}} - {{SC} \over {SC'}} = {{SA} \over {SA'}} + {{SB} \over {SB'}} = 2 + 2 = 4$ (do A’, B’ lần lượt là trung điểm của SA, AB).