Bài 9.28 (SGK trang 81): Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Đáp án
Lời giải chi tiết
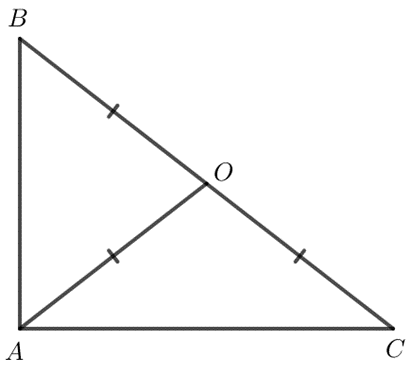
Hình vẽ minh họa:
Giả sử O nằm trên cạnh BC.
Ta có: ∆OAB cân tại O (vì OA = OB) nên
∆OAC cân tại O (Vì OA = OC) nên
Cộng vế với vế, ta được:
Xét tam giác ABC ta có:
=> Tam giác ABC vuông tại A.
Vậy nếu O nằm trên một cạnh của tam giác ABC và O cách đều ba đỉnh của tam giác ABC thì ABC là một tam giác vuông.


