Đường cao trong tam giác cân
I. Lý thuyết
Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình trên:
Công thức tính đường cao AH:
Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên:
⇒ HB=HC= ½BC
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
AH²+BH²=AB²
⇒AH²=AB²−BH²
II. Ví dụ minh họa
Ví dụ 1: Cho Δ ABC cân tại A có BC = 30(cm), đường cao AH = 20(cm). Tính đường cao ứng với cạnh bên của tam giác cân đó.
Giải:
Xét Δ ABC cân tại A có BC = 30(cm)
⇒ BH = CH = 15(cm).
Áp dụng đinh lý Py – ta – go ta có:
Kẻ , giờ ta phải tính BK = ?
Ta có:
Mặt khác
Do đó, ta có ⇔
Ví dụ 2: Cho ΔABC cân tại A, trung tuyến AM. Biết BC = 24cm, AM = 5cm. Tính độ dài các cạnh AB và AC
A. AB = AC = 13cm
B. AB = AC = 14cm
C. AB = AC = 15cm
D. AB = AC = 16cm
Giải:
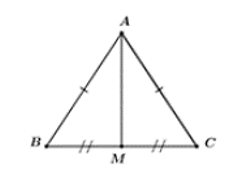
ΔABC cân tại A (gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó.
Vì AM là trung tuyến của ΔABC nên M là trung điểm của BC
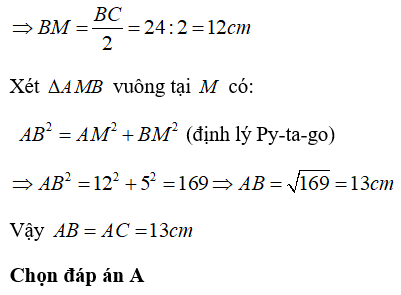
III. Bài tập vận dụng
Bài 1: Cho tam giác ABC cân tại A, AB = AC = 4 cm, BC = 14 cm. Kẻ AH vuông góc với BC tại H. Tính AH:
Giải:
𝐴𝐻=𝐴𝐵2−(𝐵𝐶2)2=42−72=3𝑐𝑚
Bài 2: Cho tam giác DEF cân tại D, DE = DF = 5 cm, EF = 12 cm. Kẻ DI vuông góc với EF tại I. Tính DI:
Giải:
𝐷𝐼=𝐷𝐸2−(𝐸𝐹2)2=52−62=1𝑐𝑚.
Bài 3: Cho tam giác ABC cân tại A, độ dài cạnh AB là 5 cm, cạnh đáy BC là 6 cm. Tính độ dài đường cao AH.
Giải:
Kẻ AH vuông góc với BC tại H. Áp dụng định lý Pythagoras cho tam giác ABH, ta có:
𝐴𝐻2=𝐴𝐵2−𝐵𝐻2
𝐵𝐻=𝐵𝐶2=3cm𝐴𝐻=𝐴𝐵2−𝐵𝐻2=52−32=16=4cm
Bài 4: Cho tam giác ABC cân tại A, có đường cao AH, biết AB = AC = 5; BC = 4 cm. Hãy tính độ dài đường cao AH và diện tích của tam giác ABC.
Bài 5: Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH kể từ A cắt BC tại H và tính diện tích ABC.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung giải trí học tập và các kiến thức thú vị khác tại đây.




