Đường phân giác trong tam giác vuông

Đường phân giác trong tam giác vuông

I. Lý thuyết

Trong tam giác vuông, đường phân giác của góc vuông có những tính chất đặc biệt và quan trọng, liên quan đến các tỉ số của các cạnh và cách chúng chia tam giác.

• Định nghĩa: Đường phân giác của góc vuông trong tam giác vuông là đường thẳng đi qua đỉnh góc vuông và chia đôi góc đó.
• Tính chất: Đường phân giác của góc vuông trong tam giác vuông chia cạnh huyền thành hai đoạn thẳng bằng nhau.
• Công thức liên quan: Nếu đường phân giác xuất phát từ góc vuông chia cạnh huyền là AB thành hai phần bằng nhau, thì 𝐴𝐵=2⋅𝐴𝐷, với D là điểm chia đôi cạnh huyền.

II. Ví dụ minh họa

Ví dụ 1: Tam giác ABC có AB = 6cm, AC = 9cm, BC = 10cm, đường phân giác trong AD, đường phân giác ngoài AE. Tính các độ dài DB, EB.

Lời giải

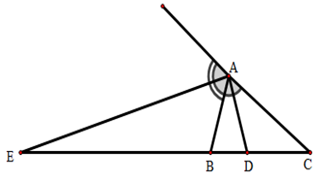
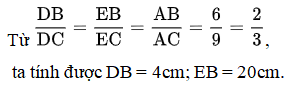
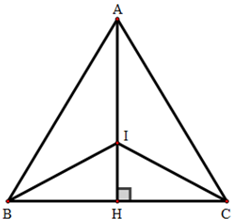
Ví dụ 2: Cho tam giác ABC cân tại A, AB = 10cm, BC = 12cm. Gọi I là giao điểm các đường phân giác của tam giác. Tính độ dài AI.

Lời giải

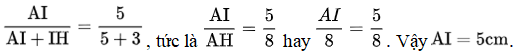
III. Bài tập vận dụng

Bài 1. Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.

Lời giải

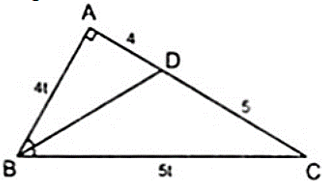
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:

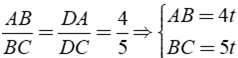
với t > 0

Áp dụng định lý Py – ta – go ta có:

BC² = AC² + AB² hay (5t)² = 92 + (4t)² ⇔ (3t)² = 92 ⇒ t = 3 (vì t > 0)

Khi đó: AB = 12cm, BC = 15cm

Bài 2: Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.

Lời giải

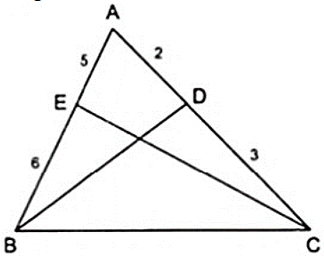
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:

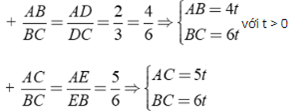
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3

Vậy AB = 12cm; BC = 18cm; AC = 15cm

Bài 3: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:

Giải:

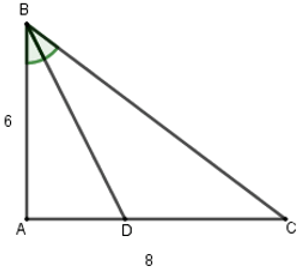
Tam giác ABC vuông tại A, áp dụng định lý Pytago có: BC² = AB² + AC²

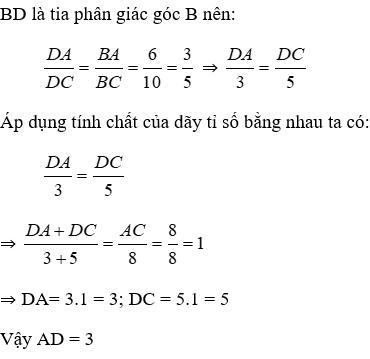
Bài 4: Cho tam giác ABC, 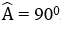, AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của 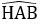cắt HB tại D. Tia phân giác của 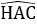cắt HC tại E. Tính DH?

Giải:

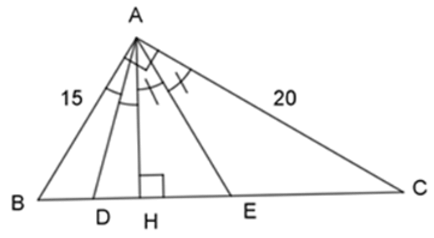
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:

AB² + AC² = BC²

⇔ 15² + 20² = BC² ⇒ BC = 25

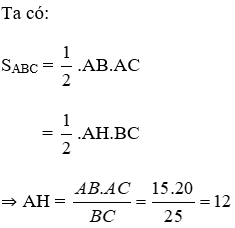
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:

AB² = AH² + HB²

⇔ 15² = 12² + HB²

⇒ HB² = 81 ⇒ HB = 9

⇒ HC = BC – HB = 25 – 9 = 16

Vì AD là phân giác của tam giác ABH nên:

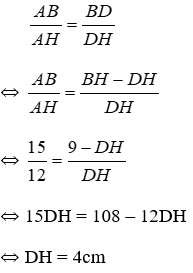
Bài 5: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D.

a) Tính BC, DB, DC.

b) Vẽ đường cao AH. Tính AH, HD và AD.

Lời giải:

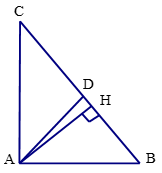
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:

BC2=AC2+AB2 suy ra BC = 5 cm

AD là tia phân giác góc A nên DBDC=ABAC suy ra DB5-DB=34

⇒4DB=15-3DB⇒DB=157(cm).

Do đó DC=BC-DB=5-157=207(cm).

Vậy BC = 5 cm, DB=157cm, DC=207cm

b) Ta có: SABC=12AB.AC=12AH.BC

⇒AH=AB.ACBC=3.45=125(cm)

Tam giác ABH vuông tại H nên

HB=AB2-AH2=32-1252=95(cm)

Ta có: HD=DB-HB=157-95=1235(cm)

Tam giác ABH vuông tại H nên

AD=HD2+AH2=12352+1252=1227 cm

Vậy AH=125cm, HD=1235cm, AD=1227cm.

Bài 6: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 6 cm. Gọi E là trung điểm AC, tia phân giác của góc A cắt BC tại D.

a. Tính BC?

b. Chứng minh: tam giác BAD = tam giác EAD

c. Gọi H và K lần lượt là hình chiếu của G trên Ab, AC. Chứng minh rằng: điểm D cách đều AB và AC.

Giải

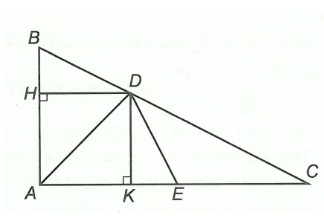
a. Xét tam giác ABC vuông tại A, ta có:

AB^2 + AC^2 = BC^2 (định lý pytago)

=> BC = căn bậc hai của 45 (cm)

b. Vì E là trung điểm của AC nên:

AE = 1/2 AC = 3cm => AE = AB

Xét tam giác BAD và tam giác EAD có:

góc BAd = góc EAD (AD là phân giác)

AD chung

AB = AE (chứng minh tên)

Do đó, tam giác BAD = tam giác EAD (cgc)

c. Vì D nằm trên tia phân giác của góc BAC nên DH = DK (tính chất tia phân giác của một góc)

Vậy điểm D cách đều AB và AC.