Bài viết Bài tập số phức hay và khó chọn lọc bao gồm 18 câu hỏi bài tập có lời giải chi tiết với các dạng bài tập về Số phức lớp 12 từ cơ bản đến nâng cao giúp học sinh lớp 12 biết cách làm bài tập Số phức.
Câu 1. Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho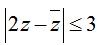 
, và số phức z có phần ảo không âm. Tính diện tích hình H.
Lời giải:
Đáp án : C
Giải thích :
Gọi z = x + yi.
Ta có:
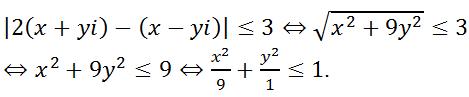
Suy ra tập hợp điểm biểu diễn số phức z là miền trong của Elip:
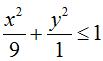
Ta có a = 3; b = 1 nên diện tích hình H cần tìm bằng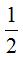 
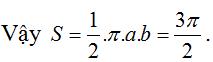
diện tích Elip
Câu 2. Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa đọ Oxy để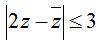 
số phức z có phần thực không âm. Tính diện tích hình (H).
Lời giải:
Đáp án : A
Giải thích :
Giả sử z = a + bi khi đó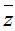 
= a – bi
Giả thiết của bài toán là:
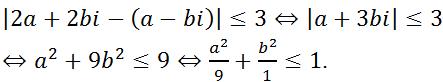
Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a;b) thuộc miền trong của elip:
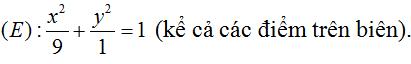
+ Bán trục lớn của (E) là a’ = 3, bán trục bé của(E )là b’ = 1 nên diện tích cần tính của miền (H) là
S = πa’b’ = 3π
Câu 3. Cho số phức z thỏa mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 + 2i|.
A. maxP = 8; minP = √39. B.maxP = 10; minP = √39.
C. maxP = 8; minP = 6. D. max P = 10; minP = 6
Lời giải:
Đáp án : A
Giải thích :
Ta có:
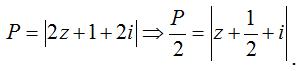
Ta chỉ cần tìm GTLN, GTNN của
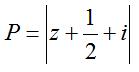
Ta thấy z1 = 1 – 3i; z2 = -2 + i và z0 =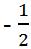 
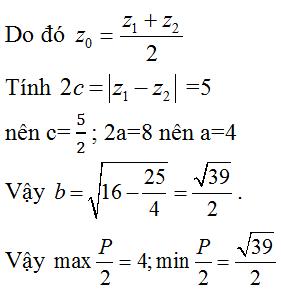
-i
Do đó max P = 8; min P = √39 .
Câu 4. Cho số phức z thỏa mãn:
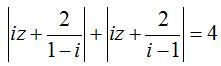
Gọi M vàm n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z| . Tính M.n.
A. 2. B. 1. C. 2√2. D. 2√3.
Lời giải:
Đáp án : C
Giải thích :
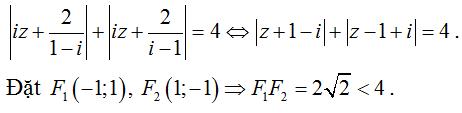
Suy ra quỹ tích điểm biểu diễn số phức z là elíp có tiêu điểm và độ dài trục lớn là 2a = 4 và tiêu cự 2c = 2√2.
Khi đó:
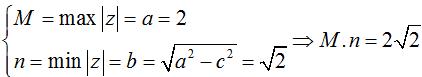
Câu 5. Cho số phức z = a + bi, (a ≥ 0; b ≥ 0; a, b ∈ R). Đặt f(x) = ax2 + bx – 2. Biết:
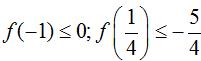
Tính giá trị lớn nhất của |z| .
A. max|z| = 2√5 B. max|z| = 3√2
C. max|z| = 5 D. max|z| = 2√6
Lời giải:
Đáp án : A
Giải thích :
Từ giả thiết ta có:
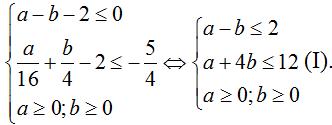
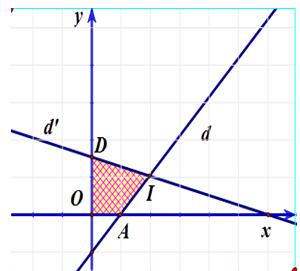
Xét trên hệ tọa độ Oxy các đường thẳng
d: x – y – 2 = 0; d’: x + 4y – 12 = 0 và các trục tọa độ
+ Đường thẳng d ∩ Ox = A(2; 0); d ∩ Oy = (0; -2) = B; d’ ∩ Ox = C(12; 0) và hai đường thẳng d ∩ d’ = I(4; 2)
+ Miền nghiệm của (I) được biểu diễn trên mặt phẳng tọa độ nằm trong tứ giác OAID kể cả các điểm thuộc trên các cạnh của đa giác.
+ Ta có: |z|2 = a2 + b2 = OM2, |z| lớn nhất khi và chỉ khi OM lớn nhất hay OM2 lớn nhất với M(a; b) là điểm thuộc miền đa giác lồi OAID.
+ Ta có: OA = 2; OI = 2√5; OD = 3. Từ đó suy ra max|z| = 2√5
Dấu bằng diễn ra khi và chỉ khi z = 4 + 2i.
Câu 6. Tập hợp các điểm biểu diễn số phức z thỏa
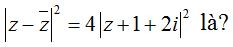
A. Một parabol. B. Một điểm. C. Một đường thẳng. D. Một đường tròn.
Lời giải:
Đáp án : A
Giải thích :
Giả sử z = x + yi, (x, y ∈ R), khi đó ta có: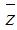 
= x – yi
Từ đó ta được:
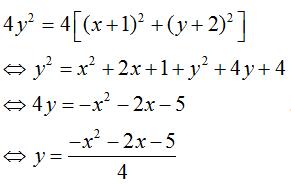
Vậy quỹ tích cần tìm là đường parabol.
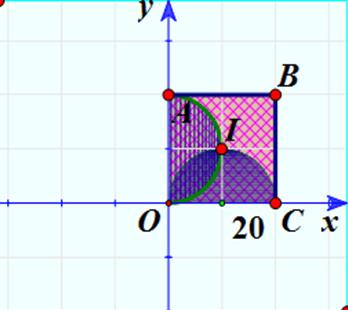
Câu 7. Trong mặt phẳng tọa độ Oxy, gọi H là phần mặt phẳng chứa các điểm biểu diễn của các số phức z thỏa mãn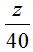 
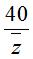
và 
có phần thực và ảo đều thuộc [0; 1] . Tính diện tích của H
A. 1600. B. 400π. C. 50(3 – π). D. 1200- 200π .
Lời giải:
Đáp án : D
Giải thích :
+ Giả sử z = x + yi, (x, y ∈ R), khi đó:
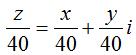
theo bài ta có: 0 ≤ x ≤ 40; 0 ≤ y ≤ 40.
Từ đó ta thấy điểm biểu diễn M cho các số phức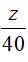 
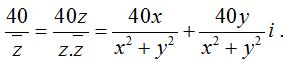
là hình vuông có OABC như hình vẽ.
Theo bài ta có:
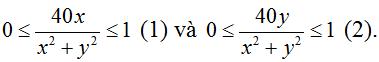
Từ (1) ta được x ≥ 0 và x2 + y2 ≥ 40x <=> (x – 20)2 + y2 ≥ 400 (1′).
Từ (2) ta được y ≥ 0 và x2 + y2 ≥ 40y <=> x2 + (y – 20)2 ≥ 400 (2′)
Tập hợp các điểm biểu diễn cho miền (H) là nằm trong miền “màu đỏ” ta cần tính diện tích của miền này.
+ Diện tích của một phần bốn cung tròn có bán kính R = 20 là:
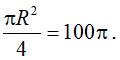
Nên diện tích hình hoa văn tạo bởi cung AIO và cung OIC là S* = 100π + 202 + 100π = 400 + 200π và diện tích cần tính bằng: S = 402 – S* = 1200 – 200π.
Câu 8. Cho hai số phức z1, z2 thỏa mãn |z1| = 2, |z2| = √3 và nếu gọi M, N lần lượt là điểm biểu diễn cho các số phức z1; z2 thì:
A. P = √5. B. P = 4√7. C. P = 3√3. D. P = 5√2.
Lời giải:
Đáp án : B
Giải thích :
Ta có:
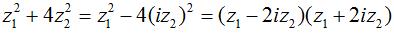
Từ đó ta có: P = |z1 – 2iz2|.|z1 + 2iz2|.
Theo bài gọi điểm biểu diễn cho số phức 2iz là A khi đó N là trung điểm của đoạn OA.
Ta có:
|z1 – 2iz| = MA, theo định lý cô sin cho tam giác OMA ta có:
MA2 = OM2 + OA2 – 2OM.OA.cos30o = 4 + 4.4 – 2.2.2√3.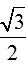
= 4
Từ đó ta được MA = 2.
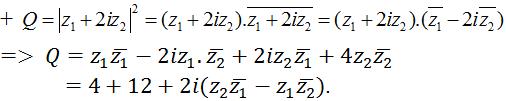
Nếu đặt z1 = a + bi; z2 = x + yi, (a, b, x, y ∈ R), ta có:
Q = 16 + 2i[(x + yi)(a – bi) – (a + bi)(x – yi)] = 16 + 2i(-2bxi + 2ayi) = 16 + 4(bx – ay)
Ta có: iz2 = -y + xi nên ta có:
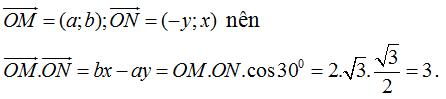
Từ đó ta được Q = 16 + 4.3 = 28, từ đó suy ra |z1 + 2iz2| = 2√7. Từ đó ta được P = 4√7.
Câu 9: Cho số phức z thỏa mãn |z + 2 – i| + |z – 4 -7i| = 6√2. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P = |z – 1 + i|. Giá trị của tổng S = M + m là:
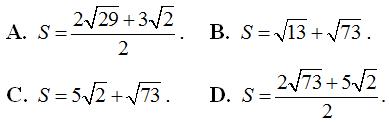
Lời giải:
Đáp án : D
Giải thích :
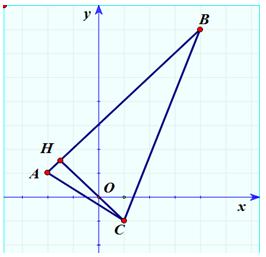
Cách 1: Dùng hình học
+ Đặt z = a + bi, khi đó điểm biểu diễn cho số phức z là M(a; b).
Gọi A(-2; 1); B(4; 7) lần lượt là điểm biểu diễn cho các số phức z1 = -2 + i và z2 = 4 + 7i, khi đó giả thiết là MA + MB = 6√2 mà AB = 6√2 nên từ đây suy ra M ∈ AB (đoạn).
+ Phương trình đường thẳng AB: x – y + 3 = 0 từ đó đoạn AB có phương trình như trên tuy nhiên x ∈ [-2; 4] .
+ Gọi C(1; -1) khi đó ta có:P = MC, với M thuộc đoạn AB
+ min MC = MH = d(C, AB) =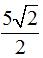 
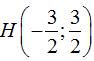
đạt được khi 
thuộc đoạn AB.
+ max MC = max{MA, MB} = max{√13, √73} = √73
+ Vậy đáp số là:
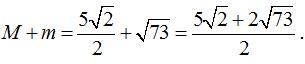
Chọn D.
Cách 2: Dùng hình học và đại số
+ Đặt z = a + bi, khi đó điểm biểu diễn cho số phức z là M(a; b).
Gọi A(-2;1); B(4;7) lần lượt là điểm biểu diễn cho các số phức z1 = -2 + i và z2 = 4 + 7i, khi đó giả thiết là MA + MB = 6√2 mà AB = 6√2 nên từ đây suy ra M ∈ AB (đoạn).
Vì M ∈ [AB] nên M(a; a + 3); a ∈ [-2; 4] (vì AB: x – y + 3 = 0).
+ Khi đó ta có:
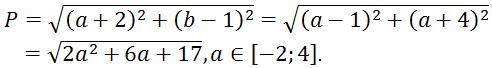
Khảo sát hàm số trên ta được kết quả như trên.
Cách 3: Dùng bất đẳng thức mincopxki, như sau:
Giả sử z = a + bi, khi đó ta có:
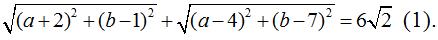
Từ đó ta có:
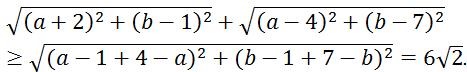
Dấu bằng xảy ra khi và chỉ khi:
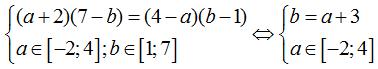
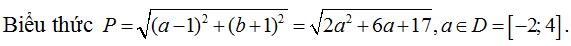
Khảo sát hàm số từ đó tìm được kết quả của bài toán.
Câu 10. Trong mặt phẳng phức Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn:
là hai đường thẳng d1 ; d2. Khoảng cách giữa 2 đường thẳng d1 ; d2 là bao nhiêu?
A. d(d1 ; d2) = 2. B. d(d1 ; d2) = 4. C. d(d1 ; d2) = 1. D. d(d1 ; d2) = 6.
Lời giải:
Đáp án : B
Giải thích :
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi
Ta có:
⇔ |x2 + 2xyi – y2 + x2 – 2xyi – y2 + 2x2 + 2y2| = 16
⇔ | 4x2| = 16 ⇔ x = ± 2
=< d(d1 ; d2)=4.
Câu 11. Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để 
số phức z có phần thực không âm. Tính diện tích hình (H).
Lời giải:
Đáp án : A
Giải thích :
Giả sử z = a + bi , khi đó 
, giả thiết của bài toán là
|2a + 2bi – (a – bi)| ≤ 3 ⇔ |a + 3bi| ≤ 3 ⇔ a2 + 9b2
Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a;b) thuộc miền trong của elip:
(kể cả các điểm trên biên).
+ Bán trục lớn của (E) là a = 3, bán trục bé của (E) là b = 1 nên diện tích cần tính của miền (H) là S = πab = 3π .
Câu 12. Cho số phức z thỏa mãn điều kiện |z – 1| = √2. Tìm giá trị lớn nhất của T = | z + i| + |z – 2 – i|
A. max T = 8√2. B. max T = 4 . C. max T = 4√2. D. maxT = 8 .
Lời giải:
Đáp án : B
Giải thích :
T = | z + i| + |z – 2 – i| = |(z – 1) + (1 + i)| + |(z – 1) – (1 + i)|
Đặt w = z – 1. Ta có |w| = 1 và T = |w + (1 + i)| + |w – (1 + i)|
Đặt w = x + yi . Khi đó |w|2 = 1 = x2 + y2
Vậy maxT = 4 .
Câu 13. Cho số phức z thoả mãn |z| = 1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z + 1| + |z2 – z + 1|. Tính giá trị của M.n
Lời giải:
Đáp án : A
Giải thích :
Cách 1:
Re(z) là phần thực của số phức z, Im(z) là phần ảo của số phức z, |z| = 1 nên z.
= 1
Đặt t = |z + 1|, ta có: 0 = |z| – 1 ≥ |z + 1| ≥ |z| + 1 = 2 => t ∈ [0; 2]
Xét hàm số: f(t) = t + |t2 – 3|; t ∈ [0; 2].
Xét 2 TH:
Cách 2:
z = r(cosx + isinx) = a + bi
Câu 14. Cho số phức z thoả mãn |z – 3 – 4i| = √5. Gọi M và m là giá trị lớn nhất và giá trị nhỉ nhất của biểu thức P = |z + 2|2 – |z – i|2. Tính module số phức w = M + mi
Lời giải:
Đáp án : B
Giải thích :
Cách 1:
f'(x) = 8(x – 3) – 8(P – 4x – 11) = 0
⇔ x = 0,2P – 1,6
=> y = 0,1P + 1,7
Thay vào f(x) ta được:
Cách 2:
|z – 3 – 4i| = √5. Nên (x – 3)2 + (y – 4)2 = 5 (C)
Δ 4x + 2y + 3 – P = 0. Tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
⇔ d(I; Δ) ≤ R ⇔ |23 – P| ≤ 10 ⇔ 13 ≤ P ≤ 33
Vậy Max P = 33; MinP = 12
Câu 15. Cho số phức z thoả mãn|z| = 1. Gọi M và m là giá trị lớn nhất và nhỏ nhất của biểu thức:
Tính M + m
Lời giải:
Đáp án : D
Giải thích :
Vậy minP = 
; maxP = 3 khi t = 2
M + n = 
Câu 16 . Cho ba số phức z1; z2; z3 thoả mãn hệ:
Tính giá trị của biểu thức: T = |az1 + zb2 + cz3|
Lời giải:
Ta có 0 = sinx + siny + sin(-x – y)
Suy ra hoặc x = k2π hoặc y = k2π hoặc x + y= k2π do đó hai trong ba số z1; z2; z3 bằng nhau.
Vậy T nhận một trong ba giá trị sau:
Câu 17. Cho số phức z thay đổi và thỏa mãn |z – 1 – i| = 5. Tìm giá trị lớn nhất của biểu thức P = 2|z – 8i| – |z – 7- 9i|
Lời giải:
Gọi M(x ; y) biểu diễn số phức z, từ |z – 1 – i| = 5 thì M nằm trên đường tròn
(x – 1)2 + (y – 1)2 = 25 có tâm và bán kính :I(1 ;1) và R = 5.
Gọi A(0 ;8) ; B(7 ; 9) thì
Phân tích : mục tiêu tìm tọa độ điểm sao cho MB = 2MC, nhận thấy IB = 2IM = 2R nên ta có hai cách tìm tọa độ điểm C như sau :
Cách 1 :
(x – 1)2 + (y – 1)2 = 25 ⇔ T = x2 + y2 – 23 = 0
Nên chọn điểm 
thì MB = 2MC
Cách 2 : Lấy điểm C thỏa mãn 
thì tam giác đồng dạng với tam giác IBM nên ta có MB = 2MC, từ đó
Ta có : P = 2MA – MB = 2(MA – MC) ≤ 2AC = 5√5
Dấu “=” đạt được khi điểm C nằm trên đoạn AM.
Câu 18. Cho số phức z thoả mãn:
Giá trị lớn nhất của biểu thức P = |z – 5 – 2i| bằng
A. √2 + 5√3 B. √2 + 3√5
C. √5 + 2√3 D. √5 + 3√2
Lời giải:
Đáp án : B
Giải thích :
Cách 1: Đại số
Đặt z = a + bi.
Từ giả thiết
Dễ thấy P lớn nhất khi ab ≤ 0.
Khi đó :
Do a;b ≤ 0 nên từ (1) ta có (a + 1)2 + (b + 1)2 = 2.
Suy ra
Dấu “=” xảy ra khi
Chọn B.
Cách 2: Hình học
Đặt z = a + bi.
Từ giả thiết
Tập hợp M biểu diễn z thuộc các phần đường tròn cùng bán kính là R = √2 có tâm là A(-1;1); B(1;1); C(1;-1); D(-1; -1) nằm chọn vẹn trong 1 góc phần tư (bỏ đi các cung nhỏ).
P = ME với E(5;2). Từ hình vẽ ta thấy max P = HE = ED + radic;2 = 3√5 + √2 .
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây. Chúc các bạn lướt web vui vẻ !
