Các cách chứng minh hai mặt phẳng vuông góc
I. Lý thuyết
1. Định nghĩa
Hai mặt phẳng vuông góc là hai mặt phẳng có góc giữa của chúng bằng 90o
2. Điều kiện
Hai mặt phẳng vuông góc với nhau khi và chỉ khi một mặt phẳng có chứa đường thẳng vuông góc với mặt phẳng còn lại
3. Tính chất
– Trong trường hợp nếu 2 mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến của 2 mặt phẳng thì sẽ vuông góc với mặt phẳng kia
– Nếu mặt phẳng (A), (B) vuông góc với nhau thì đường thẳng a đi qua điểm H (với điểm H nằm trên mặt phẳng A) và vuông góc với (B) sẽ nằm trong (A).
– Nếu hai mặt phẳng cắt nhau và 2 mặt phẳng này cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng vuông góc với mặt phẳng còn lại.
4. Cách chứng minh
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ⊥ (Q), ta có thể chứng minh bởi một trong các cách sau:
– Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).
– Chứng minh ((P), (Q)) = 90°
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ⊥ (P), ta có thể chứng minh bởi một trong các cách sau:
– Chứng minh d ⊂ (Q) với (Q) ⊥ (P) và d vuông góc với giao tuyến c của (P) và (Q).
– Chứng minh d = (Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P).
– Sử dụng các cách chứng minh đã biết ở phần trước.
II. Ví dụ minh họa
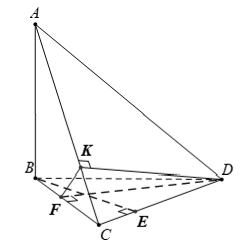
Ví dụ 1: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?
A. (ADC) ⊥ (ABE) B. (ADC) ⊥ (DFK)
C. (ADC) ⊥ (ABC) D. (BDC) ⊥ (ABE)
Hướng dẫn giải
Ta xét các phương án:
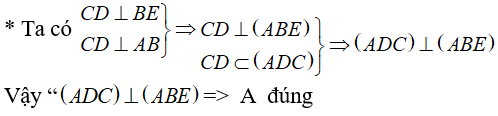
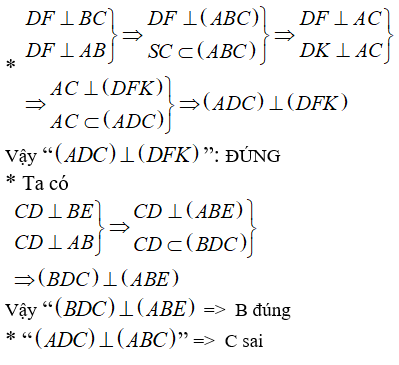
Chọn C
Ví dụ 2: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC) . Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. (ABE) ⊥ (ADC) B. (ABD) ⊥ (ADC)
C. (ABC) ⊥ (DFK) D. (DFK) ⊥ (ADC)
Hướng dẫn giải
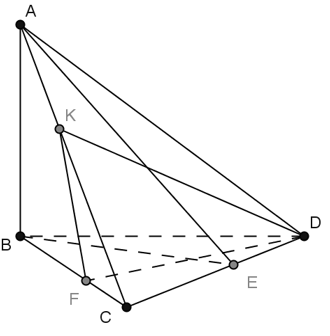
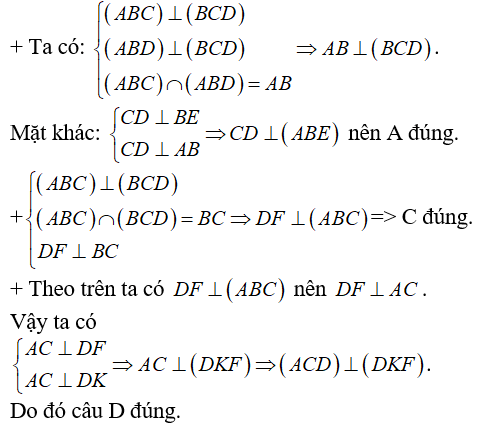
Chọn B
III. Bài tập vận dụng
Câu 1: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
A. H ∈ SB
B. H trùng với trọng tâm tam giác SBC.
C. H ∈ SC
D. H ∈ SI (I là trung điểm của BC).
Hướng dẫn giải
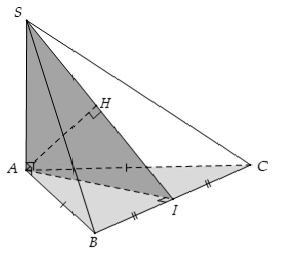
Chọn D
Gọi I là trung điểm của BC
⇒ AI ⊥ BC mà BC ⊥ SA ⇒ BC ⊥ (SAI)
⇒ SI ⊥ BC (1)
Khi đó H là hình chiếu vuông góc của A lên (SBC) .
Suy ra AH ⊥ BC
Lại có: SA ⊥ BC
⇒ BC ⊥ (SAH) ⇒ BC ⊥ SH (2)
Từ (1) và (2) suy ra 3 điểm S; H; I thẳng hàng.
Chọn D.
Câu 2: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC) . Khẳng định nào sau đây sai?
A. SC ⊥ (ABC)
B. Nếu A’ là hình chiếu vuông góc của A lên ( SBC) thì A’ ∈ SB .
C. (SAC) ⊥ (ABC)
D. BK là đường cao của tam giác ABC thì BK ⊥ (SAC)
Hướng dẫn giải
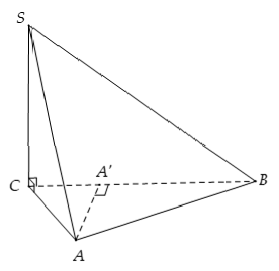
Chọn B
+ Ta có: 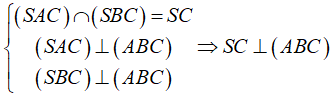
+ Gọi A’ là hình chiếu vuông góc của A lên (SBC)
khi đó AA’ ⊥ (SBC) ⇒ AA’ ⊥ BC ⇒ A’ ∈ BC
Suy ra đáp án B sai.
Chọn B.
Câu 3: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC) , tam giác ABC vuông cân ở A và có đường cao AH. Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây đúng?
A. SC ⊥ (ABC)
B. (SAH) ⊥ (SBC)
C. O ∈ SC
D. Góc giữa (SBC) và (ABC) là góc ∠SBA
Hướng dẫn giải
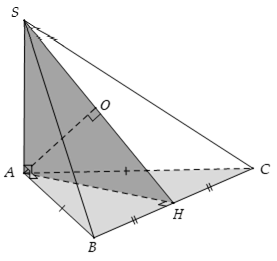
Chọn B
Ta có: 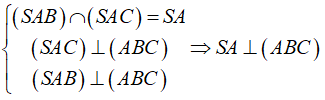
Gọi H là trung điểm của BC ⇒ AH ⊥ BC (vì tam giác ABC vuông cân tại A).
mà BC ⊥ SA ⇒ BC ⊥ (SAH) ⇒ (SBC) ⊥ (SAH)
Khi đó O là hình chiếu vuông góc của A lên (SBC)
Thì suy ra O thuộc SH và ((SBC), (ABC)) = ∠SHA
Vậy đáp án B đúng
Câu 4: Cho hình lập phương ABCD.A1B1C1D1 . Mặt phẳng (A1BD) không vuông góc với mặt phẳng nào dưới đây?
A. (AB1D) B. (ACC1A1) C. (ABD1) D. (A1BC1)
Hướng dẫn giải
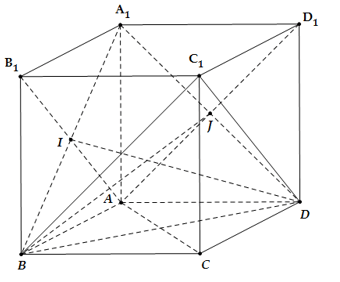
* Gọi I = AB1 ∩ A1B
Tam giác A1BD đều có DI là đường trung tuyến nên
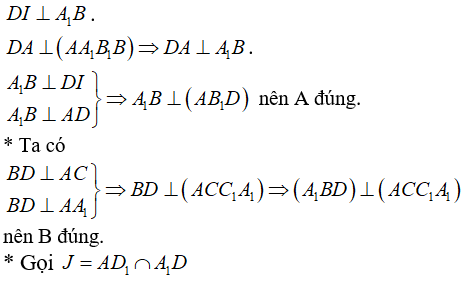
Tam giác A1BD đều có BJ là đường trung tuyến nên BJ ⊥ A1D .
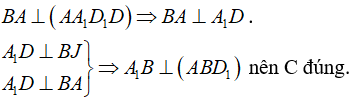
Chọn D
Câu 5: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khẳng định nào sau đây sai?
A. Tam giác AB’C là tam giác đều.
B. Nếu α là góc giữa AC’ và ( ABCD) thì cosα = √(2/3) .
C. ACC’A’ là hình chữ nhật có diện tích bằng 2a2.
D. Hai mặt (AA’C’C) và (BB’D’D) ở trong hai mặt phẳng vuông góc với nhau.
Hướng dẫn giải
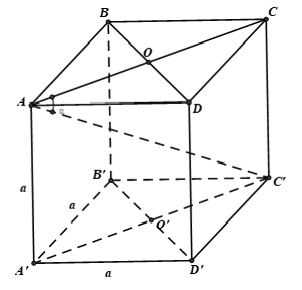
Chọn C
Từ giả thiết tính được AC = a√2
Mặt khác vì ABCD.A’B’C’D’ là hình lập phương nên suy ra ∠AA’C’ = 90°
Xét tứ giác ACC’A’ có 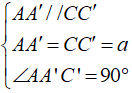
⇒ ACC’A’ là hình chữ nhật có các cạnh a và a√2.
Diện tích hình chữ nhật ACC’A’ là :
S = a.a.√2 = a2√2 (đvdt)
⇒ đáp án C sai.
Câu 6: Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Khẳng định nào sau đây sai?
A. Hai mặt ACC’A’ và BDD’B’ vuông góc nhau.
B. Bốn đường chéo AC’; A’C; BD’; B’D bằng nhau và bằng .
C. Hai mặt ACC’A’ và BDD’B’ là hai hình vuông bằng nhau.
D. AC ⊥ BD’
Lời giải:
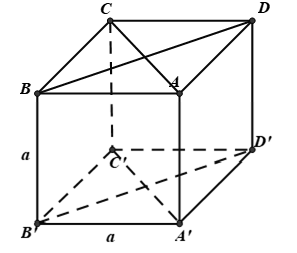
Chọn C
Vì theo giả thiết ABCD.A’B’C’D’ ta dễ dàng chỉ ra được:
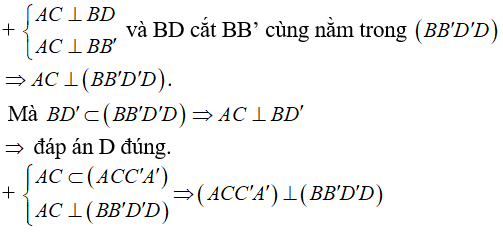
⇒ đáp án A đúng.
+ Áp dụng đình lý Pytago trong tam giác B’A’D’ vuông tại A’ ta có:
B’D’2 = B’A’2 + A’D’2 = a2 + a2 = 2a2
Áp dụng định lý Pytago trong tam giác BB’D’ vuông tại B’ ta có:
BD’2 = BB’2 + B’D’2 = a2 + 2a2 = 3a2 ⇒ BD’ = a√3
Hoàn toàn tương tự ta tính được độ dài các đường chéo còn lại của hình lập phương đều bằng nhau và bằng a√3 ⇒ đáp án B đúng.
+ Xét tứ giác ACC’A’ có
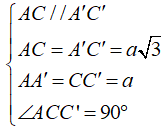
⇒ ACC’A’ là hình chữ nhật
hoàn toàn tương tự ta cũng chỉ ra BDD’B’ cũng là hình chữ nhật có các cạnh là a và a√3
Hai mặt ACC’A’ và BDD’B’ là hai hình chữ nhật bằng nhau
⇒ đáp án C sai.
Câu 7: Cho hình lăng trụ ABCD.A’B’C’D’ . Hình chiếu vuông góc của A’ lên (ABC) trùng với trực tâm H của tam giác ABC . Khẳng định nào sau đây không đúng?
A. (AA’B’B) ⊥ (BB’C’C)
B. (AA’H) ⊥ (A’B’C’)
C. BB’C’C là hình chữ nhật
D. (BB’C’C) ⊥ (AA’H)
Lời giải:
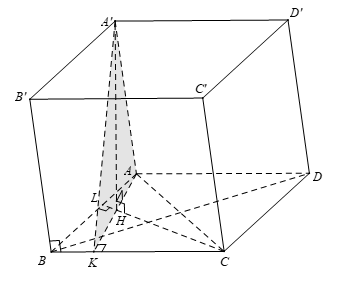
Chọn A
Gọi K là hình chiếu vuông góc của A lên BC

Câu 8: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC’) có số đo bằng 60°. Cạnh bên của hình lăng trụ bằng:
A. 3a B. a√3 C. 2a D. a√2
Lời giải:
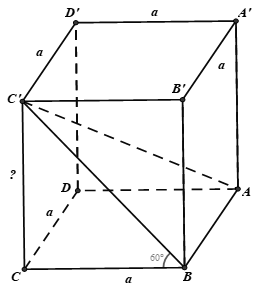
Chọn B.
Ta có: (ABCD) ∩ (ABC’) = AB
Ta có: AB ⊥ BC và AB ⊥ BB’ (vì lăng trụ đã cho là lăng trụ tứ giác đều)
⇒ AB ⊥ (BB’C’C) mà C’B ⊂ (BB’C’C) ⇒ AB ⊥ C’B
Mặt khác: CB ⊥ AB
⇒ ((ABCD), (ABC’)) = (CB, C’B) = ∠ CBC’ = 60°
Áp dụng hệ thức lượng trong tam giác BCC’ vuông tại C ta có:
tan(CBC’) = CC’/CB ⇒ CC’ = CB.tan(CBC’) = a.tan60° = a√3
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung giải trí học tập và các kiến thức thú vị khác tại đây.




