Điều kiện của hàm số mũ

Điều kiện của hàm số mũ

I. Lý thuyết

Để tìm tập xác định của hàm số mũ, ta cần xác định điều kiện để hàm số có nghĩa. Hàm số mũ y = a^x với a > 0 và a ≠ 1 có tập xác định là R (toàn bộ trục số thực). Tuy nhiên, đối với các hàm số mũ phức tạp hơn như y = a^u(x), ta cần tìm điều kiện để hàm số u(x) xác định.

II. Ví dụ minh họa

Ví dụ 1: Tìm tập xác định của hàm số y = (x² – 1)^-8

Hàm số xác định khi và chỉ khi x² – 1 ≠ 0, tức là:

𝑥2−1≠0⇔𝑥≠±1

Vậy tập xác định của hàm số là:

𝐷=𝑅∖{−1,1}

Ví dụ 2: Tìm tập xác định của hàm số y = (1 – 2x)^{√3 – 1}

Hàm số xác định khi 1 – 2x > 0, tức là:

1−2𝑥>0⇔𝑥<12

Vậy tập xác định của hàm số là:

𝐷=(−∞,12)

III. Bài tập vận dụng

Bài 1: Tìm tập xác định của hàm số y = √(x² – 3x + 2)/(3 – x) + (2x – 5)^{√7 + 1} – 3x – 1

Để hàm số xác định, cần có:

{𝑥2−3𝑥+23−𝑥≥02𝑥−5>0

Giải hệ bất phương trình:

{𝑥≤12≤𝑥<3𝑥>52

Vậy tập xác định của hàm số là:

𝐷=(52,3)

Bài 2: Tìm tập xác định của hàm số y = log(x² – 6x + 5)

Hàm số xác định khi x² – 6x + 5 > 0:

𝑥2−6𝑥+5>0

Giải phương trình:

(𝑥−1)(𝑥−5)>0

Vậy tập xác định của hàm số là:

𝐷=(−∞,1)∪(5,+∞)

Bài 3: Tìm tập xác định D của hàm số

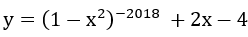
Lời giải:

Hàm số xác định khi và chỉ khi 1-x² ≠ 0 ⇔ x ≠ ±1

Bài 4: Tìm tập xác định D của hàm số

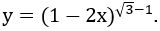
Lời giải: Hàm số xác định khi và chỉ khi 1-2x > 0 ⇔ x < 1/2

Bài 5: Tìm tập xác định D của hàm số

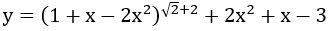
Lời giải: Hàm số xác định khi và chỉ khi 1+x-2x² > 0 ⇔ -1/2 < x < 1

Bài 6: Tìm tập xác định D của hàm số

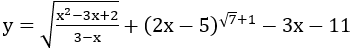
Bài 7: Tìm tập xác định D của hàm số

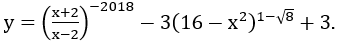
Bài 8: Tìm tập xác định D của hàm số y=(9-x2)13+log2x-1

Bài 9: Tìm tập xác định D của hàm số y=(x2-x-2)-log100