Hướng dẫn giải chi tiết Đề kiểm tra học kì 1 môn Toán lớp 11 có đáp án đề số 1 có đáp án nhanh và chính xác nhất dành cho học sinh tham khảo được tổng hợp bởi Giải bài tập. Mời các bạn học sinh cùng tham khảo.

Đề bài
I. PHẦN TRẮC NGHIỆM (20 câu – 4,0 điểm – Thời gian: 35 phút)
Câu 1 : Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số?
A. 100. B. 120.
C. 180. D. 216.
Câu 2 : Từ một nhóm học sinh gồm 6 nam, 7 nữ, chọn ngẫu nhiên 3 học sinh. Tính xác suất để trong 3 học sinh được chọn có đúng 2 nam.
A. 105286.
B. 27286.
C. 11143.
D. 63143.
Câu 3 : Cho khai triển (x+2)n. Tìm số hạng chứa x6 của khai triển biết 2C2n+3A2n−360=0.
A. 3360.
B. 3360x6.
C. 13440.
D. 13440x6.
Câu 4 : Cho đa giác đều (H) có 16 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 16 đỉnh của (H). Xác suất để 3 đỉnh được chọn tạo thành một tam giác vuông là.
A. 135. B. 110.
C. 15. D. 235.
Câu 5 : Tìm tập xác định của hàm số y=2sinx+1cosx−1.
A. D=R∖{1}.
B. D=R∖{π2+kπ,k∈Z}.
C. D=R∖{kπ,k∈Z}.
D. D=R∖{k2π,k∈Z}.
Câu 6 : Phương trình sinx+3–√cosx=2 tương đương với phương trình nào sau đây?
A. sin(x+π3)=1.
B. sin(x−π3)=1.
C. cos(x+π3)=1.
D. cos(x−π3)=1.
Câu 7 : Tìm nghiệm của phương trình cot(x−π3)=3–√3.
A. x=π3+kπ,k∈Z.
B. x=π2+k2π,k∈Z.
C. x=2π3+kπ,k∈Z.
D. x=kπ,k∈Z.
Câu 8 : Gọi S là tổng các nghiệm của phương trình (7−2cos2x)(sin4x−cos4x)+3=0 trong khoảng (−π;π). Giá trị của S là:
A. S=0.
B. S=5π3.
C. S=2π.
D. S=4π.
Câu 9 : Cho tam giác ABC có trọng tâm G, gọi I là trung điểm của BC. Trong các mệnh đề dưới đây mệnh đề nào SAI?
A. Phép vị tự tâm A tỉ số k=32 biến điểm G thành điểm I.
B. Phép vị tự tâm I tỉ số k=13 biến điểm A thành điểm G.
C. Phép vị tự tâm A tỉ số k=23 biến điểm I thành điểm G.
D. Phép vị tự tâm I tỉ số k=13 biến điểm G thành điểm A.
Câu 10 : Trong mặt phẳng Oxy, phép quay tâm O góc −90∘ biến điểm M(2;1) thành điểm N. Tìm tọa độ của điểm N.
A. N(1;−2).
B. N(1;2).
C. N(−1;2).
D. N(−1;−2).
Câu 11 : Trong mặt phẳng Oxy, gọi B=(−1;2) là ảnh của điểm A qua phép tịnh tiến theo vecto u→=(−3;1). Tìm tọa độ của điểm A.
A. A=(−2;1).
B. A=(−4;3).
C. A=(2;1).
D. A=(2;−1).
Câu 12 : Trong mặt phẳng Oxy, cho đường tròn (C) có bán kính bằng 8. Gọi đường tròn (C’) là ảnh của (C) qua phép vị tự tỉ số k = – 2. Tính bán kính R’ của đường tròn (C’).
A. R′=8.
B. R′=16.
C. R′=−16.
D. R′=4.
Câu 13 : Trong mặt phẳng Oxy, gọi đường thẳng (d) là ảnh của đường thẳng (Δ):2x−y+3=0 qua phép tịnh tiến theo vecto u→=(3;2). Tìm phương trình đường thẳng (d).
A. 2x−y+7=0.
B. 2x−y+3=0.
C. −2x+y−1=0.
D. −2x+y+1=0.
Câu 14 : Cho dãy số (un):{u1=1,u2=1un=un−1+2un−2,(n≥3,n∈N). Giá trị u4+u5 là:
A. 16. B. 20.
C. 22. D. 24.
Câu 15 : Dãy số (un)nào có công thức tổng quát dưới đây là dãy số tăng?
A. un=(−1)n(3+2n).
B. un=cosn.
C. un=(32)n.
D. un=1−2n.
Câu 16 : Cho cấp số cộng có số hạng đầu u1=2 và có công sai d=−3. Mệnh đề nào sau đây sai?
A. u10=−25.
B. u15=−40.
C. u25=−75.
D. u26=−73.
Câu 17 : Cho cấp số cộng (un) có u2+u29=40. Giá trị của S30=u1+u2+...+u30 là:
A. 640. B. 600.
C. 620. D. 500.
Câu 18 : Có bao nhiêu số tự nhiên nhỏ hơn 151 và chia hết cho 3?
A. 49. B. 50.
C. 51. D. 52.
Câu 19 : Cho mặt phẳng (P) và điểm A không thuộc (P). Số đường thẳng qua A song song (P) là:
A. 0. B. 1.
C. 2. D. Vô số.
Câu 20 : Cho hình chóp S.ABCD có ABCD là hình thang (AB // CD). M là trung điểm của SC. Giao điểm của mặt phẳng (ABM) và mặt phẳng (SCD) là đường thẳng d. Mệnh đề nào sau đây là đúng?
A. d đi qua M và song song đường thẳng SA.
B. d đi qua M và cắt đường thẳng SB.
C. d đi qua M và song song đường thẳng CD.
D. d đi qua M và cắt đường thẳng AB.
II. PHẦN TỰ LUẬN (6,0 điểm – 55 phút)
Câu 1: (2,0 điểm) . Giải các phương trình sau:
a) 2sinx−1=0.
b) sin2x−cosx+1=0
c) sinx−3–√cosx=1.
Câu 2: (1,5 điểm)
a) Một lớp học gồm 16 học sinh nam và 14 học sinh nữ. Giáo viên chủ nhiệm chọn ngẫu nhiên 6 học sinh để tham gia lớp học về “AN TOÀN GIAO THÔNG”. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam?
b) Giải phương trình: 3A2x−2−2Cx−2x−2x2+38=0
Câu 3: (2,0 điểm)
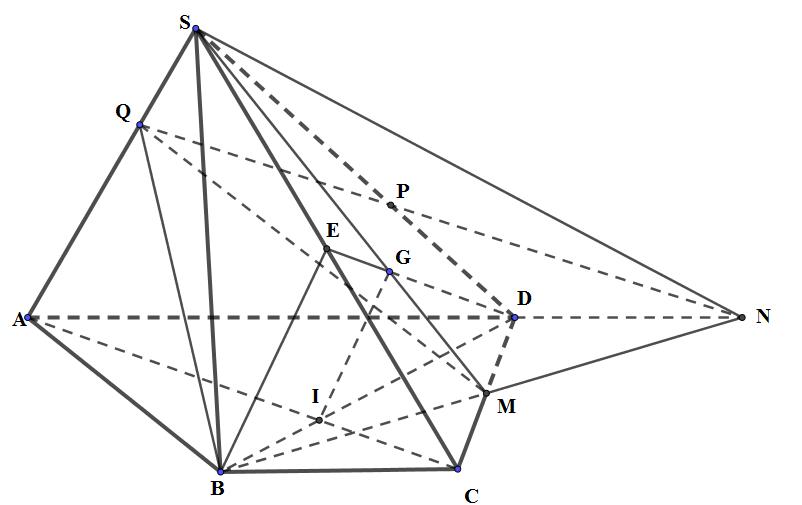
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song BC và AD = 2BC. M là trung điểm của cạnh CD, Q là điểm trên cạnh SA sao cho SA = 3SQ.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBM).
b) Gọi G là trọng tâm tam giác SCD, I là giao điểm của AC và BD. Chứng minh IG // (SBC).
c) Mặt phẳng (BMQ) cắt cạnh SD tại P. Tính tỉ số SPSD.
Câu 4: (0,5 điểm)
Tìm tất cả các giá trị của tham số m để phương trình sin2x+mcosx−4sinx−2m=0 có nghiệm.
Lời giải chi tiết
I. PHẦN TRẮC NGHIỆM (20 câu – 4,0 điểm – Thời gian: 35 phút)
|
1. D |
2. A |
3. B |
4. C |
5. D |
|
6. A |
7. C |
8. A |
9. D |
10. A |
|
11. C |
12. B |
13. D |
14. A |
15. C |
|
16. C |
17. B |
18. C |
19. D |
20. C |
II. PHẦN TỰ LUẬN (6,0 điểm – 55 phút)
Câu 1: (2,0 điểm). Giải các phương trình sau:
a)
2sinx−1=0⇔sinx=12
⇔[x=π6+k2πx=π−π6+k2π
⇔[x=π6+k2πx=5π6+k2π(k∈Z)
Vậy tập nghiệm của phương trình là: S={π6+k2π,5π6+k2π;k∈Z}.
b) sin2x−cosx+1=0
⇔1−cos2x−cosx+1=0
⇔−cos2x−cosx+2=0
⇔[cosx=1cosx=−2(vô nghiệm)
⇔x=k2π(k∈Z)
Vậy phương trình có tập nghiệm là: S={k2π;k∈Z}.
c) sinx−3–√cosx=1
⇔12sinx−3√2cosx=12
⇔cosπ3sinx−sinπ3cosx=12⇔sin(x−π3)=12⇔[x−π3=π6+k2πx−π3=π−π6+k2π⇔[x=π2+k2πx=7π6+k2π(k∈Z)
Vậy tập nghiệm của phương trình là: S={π2+k2π,7π6+k2π;k∈Z}.
Câu 2: (1,5 điểm)
Số phần tử của không gian mẫu: n(Ω)=C616+14=C630
Gọi A: “trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam”
Vì trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam nên số học sinh nam là 2, số học sinh nữ là 4.
⇒n(A)=C216C414
⇒P(A)=n(A)n(Ω)=C216C414C630=88435
b) Giải phương trình: 3A2x−2−2Cx−2x−2x2+38=0
3A2x−2−2Cx−2x−2x2+38=0,(x∈N,x⩾4)
⇔3.(x−2)!(x−4)!−2.x!(x−2)!2!−2x2+38=0⇔3(x−2)(x−3)−x(x−1)−2x2+38=0⇔3x2−15x+18−x2+x−2x2+38=0⇔−14x+56=0⇔x=4(tm)
Phương trình có tập nghiệm S={4}.
Câu 3:
a) Trong (ABCD) gọi N là giao điểm của AD và BM.
Khi đó, (SAD)∩(SBM)=SN.
b) Gọi E là trung điểm của SC.
Do G là trọng tâm tam giác SCD nên EGGD=12
Ta có: AD//BC,I=AC∩BD⇒IBID=BCAD=12
⇒EGGD=IBID=12⇒IG//BE
Mà BE⊂(SBC)⇒IG//(SBC).
c) Ta có: DN//BC,DC∩BN=M
⇒DNBC=DMMC=1
⇒DN=BC⇒DN=12AD
⇒DNAN=13
Mà SA = 3SQ ⇒SQSA=13
⇒DNAN=SQSA=13
⇒⎧⎩⎨QD//SNQNSD=23
Do DQ//SN,QN∩SD=P⇒PDSP=QDSN=23⇒SPSD=35
Câu 4: (0,5 điểm)
sin2x+mcosx−4sinx−2m=0⇔2sinxcosx−4sinx+mcosx−2m=0⇔2sinx(cosx−2)+m(cosx−2)=0⇔(cosx−2)(2sinx+m)=0⇔[cosx=2(vonghiem)sinx=−m2⇔sinx=−m2
Phương trình đã cho có nghiệm khi và chỉ khi −1≤−m2≤1⇔−2≤m≤2.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Hy vọng bài viết trên sẽ hữu ích và tác động tích cực tới kết quả học tập của bạn. Mời bạn tham khảo thêm các tài liệu học tốt khác tại đây .




