Đề kiểm tra học kì 1 môn Toán lớp 11 có đáp án đề số 2

Đề bài

A. PHẦN CÂU HỎI TRẮC NGHIỆM (5,0 điểm).

Câu 1 : Cho hình chóp $S.ABCD$ có đáy$ABCD$ là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm của SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ?

A. AD.                         B. DC.

C. EF.                         D. AB.

Câu 2 : Xét phép thử T: “Gieo một con súc sắc cân đối và đồng chất hai lần”. Xác suất để số chấm xuất hiện ở lần gieo sau lớn hơn số chấm xuất hiện ở lần gieo trước là:

A. $\dfrac{4}{9}$.                             B. $\dfrac{5}{{12}}$.

C. $\dfrac{{17}}{{36}}$.                               D. $\dfrac{1}{2}$.

Câu 3 : Cho tứ diện ABCD, điểm I nằm trong tam giác ABC, mặt phẳng $\left( \alpha  \right)$ đi qua I và song song với AB và CD. Thiết diện của tứ diện ABCD và mặt phẳng $\left( \alpha  \right)$là:

A. hình chữ nhật.

B. hình vuông.           

C. hình bình hành.

D. tam giác.

Câu 4 : Hàm số $y = \dfrac{2}{{\sin \,x}} + \dfrac{1}{{\cos x}}$ có tập xác định là

A.$R{\rm{\backslash }}\left\{ {2k\pi ,k \in Z} \right\}$.

B. $R{\rm{\backslash }}\left\{ {\dfrac{{k\pi }}{2},k \in Z} \right\}$.

C. $R{\rm{\backslash }}\left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}$.

D. $R{\rm{\backslash }}\left\{ {k\pi ,k \in Z} \right\}$.

Câu 5 : Tìm nghiệm của phương trình $\cos x = 1$.

A. $x = \pi  + k2\pi ,k \in Z$.

B. $x = \dfrac{{3\pi }}{2} + k2\pi ,k \in Z$.

C. $x = k2\pi ,k \in Z$.

D. $x = \dfrac{\pi }{2} + k2\pi ,k \in Z$.

Câu 6 : Nghiệm dương nhỏ nhất của phương trình $\tan \,x = \tan \dfrac{{6\pi }}{5}$ là:

A. $x = 6\pi$.

B. $x = \dfrac{6}{5}$.

C. $x = \dfrac{\pi }{5}$.

D. $x = \dfrac{{6\pi }}{5}$.

Câu 7 : Tổng các nghiệm của phương trình $\cos \left( {x + \dfrac{\pi }{4}} \right) = \dfrac{1}{2}$ trong khoảng $\left( { - \pi ;\pi } \right)$là:

A. $- \dfrac{\pi }{2}$.                       B. $\dfrac{\pi }{4}$.

C. $\dfrac{\pi }{2}$.                          D. $- \dfrac{{3\pi }}{2}$.

Câu 8 : Tìm tất cả các giá trị của m để phương trình $m\sin \,2x + 3\cos 2x = 5$ có nghiệm.

A. $\left| m \right| \ge 4$.

B. $\left| m \right| > 4$.

C. $m \ge 4$.

D. $m > 4$.

Câu 9 : Tập nghiệm của phương trình $\sin \,x + \sin \,2x = 0$ là:

A. $\left\{ {\dfrac{{k\pi }}{3};\pi  + k\pi ,\,k \in Z} \right\}$.

B. $\left\{ {\dfrac{{k2\pi }}{3};\pi  + k2\pi ,\,k \in Z} \right\}$.                  

C. $\left\{ {k2\pi ;\dfrac{\pi }{3} + k\dfrac{{2\pi }}{3},\,k \in Z} \right\}$.

D. $\left\{ {k2\pi ;\dfrac{\pi }{2} + k2\pi ,\,k \in Z} \right\}$.

Câu 10 : Cho hàm số $y = 2 - 3\sin 2x$. Giá trị lớn nhất của hàm số là:

A. 2.                            B. 8.

C. -1.                           D. 5.

Câu 11 : Cho hình chóp $S.ABCD$ có đáy$ABCD$ là hình thang$ABCD\left( {AD//BC} \right)$. Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng $\left( {MSB} \right)$ và $\left( {SAC} \right)$là:

A. SO (O là giao điểm của AC và BD).

B. SJ (J là giao điểm của AM và BD).

C. SI (I là giao điểm của AC và BM).

D. SP (P là giao điểm của AB và CD).

Câu 12 : Trong mặt phẳng, có bao nhiêu hình chữ nhật được tạo thành từ sáu đường thẳng đôi một song song với nhau và năm đường thẳng phân biệt cùng vuông góc với sáu đường thẳng song song đó?

A. 11.                          B. 150.           

C. 30.                          D. 600.

Câu 13 : Tìm hệ số của ${x^7}$ trong khai triển nhị thức Newton của ${\left( {2 - 3x} \right)^{10}}$.

A. -414720.

B. 414720.

C. 2099520.

D. –2099520.

Câu 14 : Trong nhóm học sinh có 15 em, chọn ngẫu nhiên 4 em trong nhóm để dự buổi văn nghệ, Hỏi có bao nhiêu cách chọn?

A. 4!                            B. 1365.

C. 32760.                    D. 15!

Câu 15 : Hàm số$y = \cos \,x$ đồng biến trên khoảng nào trong các khoảng sau đây?

A. $\left( {0;\dfrac{\pi }{2}} \right)$.

B. $\left( {\dfrac{{3\pi }}{2};2\pi } \right)$.

C. $\left( {\dfrac{\pi }{2};\pi } \right)$.

D. $\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)$.

Câu 16 : Trong mặt phẳng Oxy, cho $\overrightarrow v \left( {1; - 3} \right)$ và đường thẳng d có phương trình $2x - 3y + 5 = 0$. Phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến ${T_{\overrightarrow v }}$ là:

A. $d':\,\,2x - 3y - 6 = 0$.

B. $d':\,\,2x - 3y + 6 = 0$.

C. $d':\,\,3x - 2y - 6 = 0$.

D. $d':\,\,2x + 3y - 6 = 0$.

Câu 17 : Trong mặt phẳng Oxy, cho $\overrightarrow v \left( {2; - 1} \right)$. Hãy tìm ảnh của điểm $A\left( { - 1;2} \right)$ qua phép tịnh tiến vectơ $\overrightarrow v$.

A. $A'\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)$.    

B. $A'\left( {1;1} \right)$.

C. $A'\left( {3; - 3} \right)$.

D. $A'\left( { - 3;3} \right)$.

Câu 18 : Gọi $\alpha$là nghiệm lớn nhất thuộc khoảng $\left( {0;2\pi } \right)$của phương trình

$3\cos x + \cos 2x - \cos 3x + 1 =$$\,2\sin \,x.\sin 2x$.

Tìm $\sin 2\alpha$.

 A. $\dfrac{1}{2}$.                 B. $1$.

C. $- \dfrac{1}{2}$.              D. 0.

Câu 19 : Có 6 học sinh lớp 11 và 3 học sinh lớp 12. Tính xác suất để trong các cách sắp xếp ngẫu nhiên 9 học sinh đó vào một dãy có 9 chiếc ghế sao cho không có hai học sinh lớp 12 nào ngồi cạnh nhau.

A. $\dfrac{5}{{72}}$.                                    B. $\dfrac{7}{{12}}$.

C. $\dfrac{5}{{12}}$.                                    D. $\dfrac{1}{{1728}}$.

Câu 20 : Cho hình chóp$S.ABCD$ có đáy$ABCD$ là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là

A. SG (G là trung điểm AB).  

B. SD.            

C. SF (F là trung điểm CD).

D. SO (O là tâm hình bình hành ABCD).

Câu 21 : Hệ số của ${x^7}$ trong khai triển ${\left( {1 + 2x} \right)^n}$, với $n$là số nguyên dương thỏa mãn hệ thức $C_{n + 4}^{n + 1} - C_{n + 3}^n = 7\left( {n + 3} \right)$ là

A. ${2^7}C_{12}^7$.                        B. $C_{12}^7$.         

C. ${2^8}C_{12}^7$.                        D. ${2^7}$.

Câu 22 : Tìm số hạng không chứa x trong khai triển nhị thức Newton của ${\left( {x - \dfrac{2}{{{x^2}}}} \right)^{21}}$.

A. ${2^8}C_{21}^8$.

B. $- {2^8}C_{21}^8$.

C. ${2^7}C_{21}^7$.

D. $- {2^7}C_{21}^7$.        

Câu 23 : Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm đó ra 5 người sao cho ít nhất 1 nữ. Hỏi có bao nhiêu cách chọn?

A. $A_{20}^5 - A_{15}^5$.

B. $15504$.

C. $A_{20}^5$.        

D. $12501$.

Câu 24 : Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là

A. $\dfrac{{7!}}{{3!}}$.                                 B. 7.

C. $C_7^3$.                          D. $A_7^3$.

Câu 25 : Hệ số của số hạng chứa ${x^5}$ trong khai triển ${\left( {{x^2} + \dfrac{1}{{{x^3}}}} \right)^n}$, biết n là số nguyên dương thỏa mãn $C_n^1 + C_n^3 = 13n$.

A. 120.                                    B. 45.

C. 252.                                    D. 210.

B. PHẦN CÂU HỎI TỰ LUẬN (5,0 điểm)

Câu 1 . (1,5 điểm) Giải phương trình: $2{\sin ^2}x + 3\sqrt 2 \sin \,x + 2 = 0$.

Câu 2 . (1,5 điểm) Lấy ngẫu nhiên đồng thời 4 viên bi từ trong hộp đựng 16 viên bi trong đó có 5 viên bi màu xanh, 4 viên bi màu đỏ và 7 viên bi màu vàng. Tính xác suất để trong 4 viên bi lấy ra có đúng 2 viên bi màu vàng.

Câu 3 . (2,0 điểm) Cho hình chóp $S.ABCD$ có $ABCD$ là hình thang, đáy lớn BC với $BC = 2a,\,\,AD = AB = a$, mặt bên $\left( {SAD} \right)$là tam giác đều. Lấy điểm $M$ trên cạnh AB sao cho $MB = 2AM$. Mặt phẳng $\left( \alpha  \right)$ đi qua M và song song với SA, BC. Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng $\left( \alpha  \right)$ và tính diện tích của thiết diện đó.

Lời giải chi tiết

A. PHẦN CÂU HỎI TRẮC NGHIỆM (5,0 điểm).

 B. PHẦN CÂU HỎI TỰ LUẬN (5,0 điểm)

Câu 1.

Đặt $\sin \,x = t,\,\,\left( {t \in \left[ { - 1;1} \right]} \right)$.

Phương trình đã cho trở thành: $2{t^2} + 3\sqrt 2 t + 2 = 0$, $\Delta  = 2$ 

$\eqalign{ & \Leftrightarrow \left[ \matrix{ t = {{ - 3\sqrt 2 + \sqrt 2 } \over 4} = - {{\sqrt 2 } \over 2}\,\,\left( {tm} \right) \hfill \cr t = {{ - 3\sqrt 2 - \sqrt 2 } \over 4} = - \sqrt 2 \,\,\,\left( {ktm} \right) \hfill \cr} \right. \cr & \Rightarrow \sin \,x = - {{\sqrt 2 } \over 2} \cr & \Leftrightarrow \left[ \matrix{ x = - {\pi \over 4} + k2\pi \hfill \cr x = {{5\pi } \over 4} + k2\pi \hfill \cr} \right.,k \in Z \cr}$

Phương trình đã cho có tập nghiệm $S = \left\{ { - \dfrac{\pi }{4} + k2\pi ,k \in Z} \right\} \cup \left\{ {\dfrac{{5\pi }}{4} + k2\pi ,k \in Z} \right\}$.

Câu 2.

Số phần tử của không gian mẫu: $n\left( \Omega  \right) = C_{16}^4$

Gọi A: “trong 4 viên bi lấy ra có đúng 2 viên bi màu vàng” $ \Rightarrow n\left( A \right) = C_7^2.C_9^2$

Xác suất để trong 4 viên bi lấy ra có đúng 2 viên bi màu vàng: $P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{C_7^2.C_9^2}}{{C_{16}^4}} = \dfrac{{27}}{{65}}$.

Câu 3.

* Dựng thiết diện:

Qua M kẻ MQ song song BC ($Q \in DC$), kẻ MN song song SA  ($N \in SB$)

Qua N kẻ NP song song BC ($P \in SC$)

Khi đó, $\left( {MNPQ} \right)$ là mặt phẳng qua M và song song BC, SA

$\Rightarrow \left( {MNPQ} \right) \equiv \left( \alpha  \right)$

Thiết diện của hình chóp bị cắt bởi mặt phẳng $\left( \alpha  \right)$ là tứ giác $MNPQ$.

* Tính diện tích thiết diện:

Ta có: NP // MQ (cùng song song BC) $\Rightarrow MNPQ$ là hình thang

$\Delta SAD$ đều $ \Rightarrow SA = SD = AD = a$

ABCD là hình thang, $MQ//BC$

$\Rightarrow \dfrac{{CQ}}{{DC}} = \dfrac{{BM}}{{AB}} = \dfrac{{BN}}{{SB}} = \dfrac{2}{3}$

$MN//SA \Rightarrow \dfrac{{MN}}{{SA}} = \dfrac{{BM}}{{AB}} = \dfrac{2}{3}$ $\Rightarrow MN = \dfrac{2}{3}SA = \dfrac{2}{3}a$

$NP//BC \Rightarrow \dfrac{{NP}}{{BC}} = \dfrac{1}{3}$ $\Rightarrow NP = \dfrac{1}{3}.BC = \dfrac{2}{3}a$

$\dfrac{{PC}}{{SC}} = \dfrac{{NB}}{{SB}} = \dfrac{2}{3}$ $\Rightarrow \dfrac{{PC}}{{SC}} = \dfrac{{CQ}}{{DC}} = \dfrac{2}{3} \Rightarrow \dfrac{{PQ}}{{SD}} = \dfrac{2}{3}$ $\Rightarrow PQ = \dfrac{2}{3}SD = \dfrac{2}{3}a$

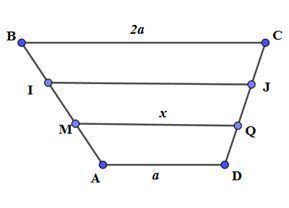
Gọi I, J lần lượt là trung điểm của BM, CQ.

Giả sử MQ có độ dài bằng x. Khi đó, do IJ là đường trung bình của hình thang BCQM 

$\Rightarrow IJ = \dfrac{{MQ + BC}}{2} = \dfrac{{x + 2a}}{2}$

Do MQ là  đường trung bình của hình thang IJDA 

$\eqalign{ & \Rightarrow 2MQ = IJ + AD \cr & \Leftrightarrow 2x = {{x + 2a} \over 2} + a \cr & \Leftrightarrow 4x = x + 2a + 2a \cr & \Leftrightarrow x = {4 \over 3}a \cr & \Rightarrow MQ = {4 \over 3}a \cr}$

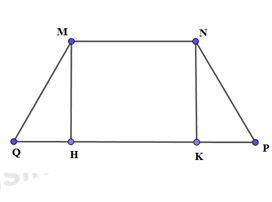
Xét hình thang MNPQ có: $NP = MN = PQ = {2 \over 3}a,\,\,MQ = {4 \over 3}a$

$\Rightarrow MNPQ$ là hình thang cân.

Kẻ MH, NK vuông góc PQ (H, K thuộc PQ)

$\Rightarrow QH = PK = \dfrac{{PQ - MN}}{2} = \dfrac{{\dfrac{4}{3}a - \dfrac{2}{3}a}}{2} = \dfrac{a}{3}$

$\Rightarrow MH = \sqrt {M{Q^2} - Q{H^2}}  = \sqrt {{{\left( {\dfrac{2}{3}a} \right)}^2} - {{\left( {\dfrac{1}{3}a} \right)}^2}}  = \sqrt {\dfrac{{{a^2}}}{3}}  = \dfrac{{a\sqrt 3 }}{3}$

Diện tích hình thang MNPQ: $S = \dfrac{1}{2}\left( {MN + PQ} \right).MH = \dfrac{1}{2}.\left( {\dfrac{2}{3}a + \dfrac{4}{3}a} \right).\dfrac{{a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 3 }}{3}$

Xem lời giải chi tiết đề thi học kì 1 tại giaibaitap.pro.vn