Điều kiện để phương trình có nghiệm
I. Lý thuyết
1. Phương Trình Bậc Hai
Để một phương trình bậc hai 𝑎𝑥2+𝑏𝑥+𝑐=0 có nghiệm, hệ số 𝑎 phải khác 0 và biệt thức Δ=𝑏2−4𝑎𝑐 cần thỏa mãn các điều kiện sau:
Nếu Δ>0, phương trình có hai nghiệm phân biệt.
Nếu Δ=0, phương trình có nghiệm kép.
Nếu Δ<0, phương trình không có nghiệm thực.
2. Phương Trình Bậc Ba
Phương trình bậc ba 𝑥3+𝑎𝑥2+𝑏𝑥+𝑐=0 có nghiệm khi hệ số của 𝑥3 khác 0. Các bước để xác định nghiệm bao gồm:
Tính Δ1=𝑏2−3𝑎𝑐 và Δ2=2𝑏3−9𝑎𝑏𝑐+27𝑎2𝑑.
Xác định 𝜖=(Δ2)2−4(Δ1)3.
Phân tích theo 𝜖:
Nếu 𝜖>0, một nghiệm thực và hai nghiệm phức.
Nếu 𝜖=0, ba nghiệm thực, có thể trùng nhau.
Nếu 𝜖<0, ba nghiệm thực.
3. Các Phương Trình Lượng Giác
Phương trình sin𝑥=𝑚 có nghiệm khi |𝑚|≤1. Tương tự, phương trình cos𝑥=𝑚 và tan𝑥=𝑚 cũng có điều kiện tương ứng về giá trị của 𝑚 để có nghiệm.
- Phương trình sin𝑥=𝑎:
- Điều kiện: |𝑎|≤1
- Nghiệm: 𝑥=sin−1(𝑎)+𝑘2𝜋 hoặc 𝑥=𝜋−sin−1(𝑎)+𝑘2𝜋, 𝑘∈𝑍
- Phương trình cos𝑥=𝑎:
- Điều kiện: |𝑎|≤1
- Nghiệm: 𝑥=cos−1(𝑎)+𝑘2𝜋 hoặc 𝑥=−cos−1(𝑎)+𝑘2𝜋, 𝑘∈𝑍
- Phương trình tan𝑥=𝑎:
- Điều kiện: Không có giới hạn đặc biệt cho 𝑎
- Nghiệm: 𝑥=tan−1(𝑎)+𝑘𝜋, 𝑘∈𝑍
- Phương trình cot𝑥=𝑎:
- Điều kiện: 𝑥≠𝑘𝜋, 𝑘∈𝑍 (do cot𝑥 không xác định tại các điểm này)
- Nghiệm: 𝑥=cot−1(𝑎)+𝑘𝜋, 𝑘∈𝑍
Việc áp dụng đúng các điều kiện và công thức nghiệm sẽ giúp
II. Ví dụ minh họa
Ví dụ 1: Cho phương trình: x2 – (2m – 1)x + m2 – 1 = 0 (x là ẩn số)
a) Tìm điều kiện của m để phương trình đã cho có hai nghiệm phân biệt.
b) Định m để hai nghiệm x1, x2 của phương trình đã cho thỏa mãn (x1 – x2)2 = x1 – 3x2
Giải
a) Δ = (2m – 1)2 – 4.(m2 – 1)= 4m2 – 4m + 1 – 4m2 + 4 = 5- 4m
Phương trình có hai nghiệm phân biệt khi Δ > 0 ⇔ 5 – 4m > 0 ⇔ m < 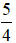
b) Phương trình có hai nghiệm ⇔ m ≤ 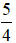
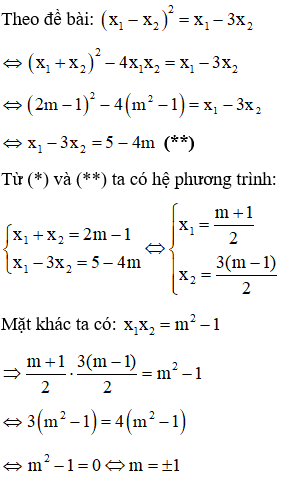
Kết hợp với điều kiện 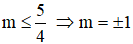 (thỏa mãn) là các giá trị cần tìm.
(thỏa mãn) là các giá trị cần tìm.
Vậy với m = 1 hoặc m = – 1 thì phương trình đã cho có 2 nghiệm x1, x2 thỏa mãn (x1 – x2)2 = x1 – 3x2.
Ví dụ 2: Cho phương trình x2 – 10mx + 9m = 0 (m là tham số)
a) Giải phương trình đã cho với m = 1.
b) Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa điều kiện x1 – 9x2 = 0.
Giải
a) Với m = 1 phương trình đã cho trở thành x2 – 10x + 9 = 0.
Ta có: a + b + c = 0 nên phương trình có hai nghiệm phân biệt là 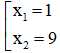
b) Δ’ = (-5m)2 – 1.9m = 25m2 – 9m
Điều kiện phương trình đã cho có hai nghiệm phân biệt là Δ’ > 0 ⇔ 25m2 – 9m > 0
Theo hệ thức Vi-ét ta có 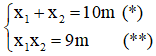
Từ (*) và giả thiết ta có hệ phương trình:
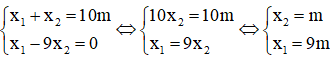
Thay vào phương trình (**) ta có:
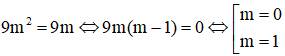
Với m = 0 ta có Δ’ = 25m2 – 9m = 0 không thỏa mãn điều kiện phương trình có 2 nghiệm phân biệt.
Với m = 1 ta có Δ’ = 25m2 – 9m = 16 > 0 thỏa mãn điều kiện để phương trình có 2 nghiệm phân biệt.
Kết luận: Vậy với m = 1thì phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa điều kiện x1-9x2 = 0
III. Bài tập vận dụng
Bài 1: Cho phương trình x2 – 2(m – 1)x + 2m – 5 = 0 (m là tham số).
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi m.
b) Tìm giá trị của m để phương trình có hai nghiệm x1, x2 thỏa mãn x1 < 1 < x2
Giải
a) Ta có: Δ = [-2(m – 1)]2 – 4.1.(2m – 5) = 4m2 – 12m + 22
= (2m)2 – 2.2m.3 + 9 + 13 = (2m-3)2 + 13 > 0 (luôn đúng với mọi m)
Vậy phương trình luôn có hai nghiệm phân biệt với mọi m.
b) Theo hệ thức Vi-ét, ta có: 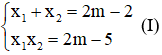
Ta có: x1 < 1 < x2 ⇒ 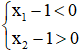 ⇒(x1 – 1)(x2 – 1) < 0⇒x1 x2 – (x1+x2)+1 < 0 (II)
⇒(x1 – 1)(x2 – 1) < 0⇒x1 x2 – (x1+x2)+1 < 0 (II)
Thay (I) vào (II) ta có: (2m – 5) – (2m – 2) + 1 < 0 ⇔ 0.m – 2 < 0 (đúng với mọi m).
Vậy với mọi m thì phương trình trên có hai nghiệm x1, x2 thỏa mãn x1 < 1 < x2
Bài 2: Cho phương trình x2 – (2m + 2)x + 2m = 0 (m là tham số). Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn 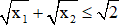
Giải
Phương trình x2 – (2m + 2)x + 2m = 0 ⇔ x2 – 2(m + 1)x + 2m = 0
Điều kiện PT có 2 nghiệm không âm x1, x2 là
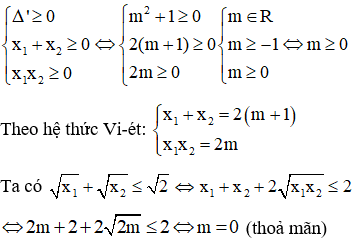
Vậy m = 0 là giá trị cần tìm.
Bài 3: Cho phương trình x2 + 2x – m2 – 1 = 0 (m là tham số)
Tìm m để phương trình trên có hai nghiệm thỏa mãn x1 = -3x2
Giải:
Ta có: Δ’ = 12 – 1.(-m2 – 1)=1 + m2 + 1 = m2 + 2 > 0 (luôn đúng với mọi m)
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m.
Theo Vi-ét ta có: 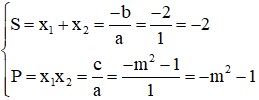
Ta có: x1 + x2 = -2 (do trên) và x1 = -3x2 nên có hệ phương trình sau:
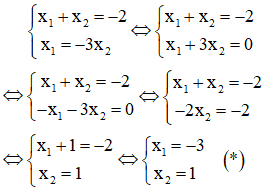
Thay (*) vào biểu thức x1.x2 = -m2 – 1 ta được:
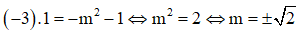
Vậy m = ±√2 là các giá trị cần tìm.
Bài 4: Cho phương trình x2 – 2(m + 1)x + m2 + m – 1 = 0 (m là tham số)
Gọi S là tập tất cả các giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện 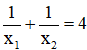 . Tính tích của các giá trị đó
. Tính tích của các giá trị đó
Giải:
Δ’ = (m + 1)2 – (m2 + m – 1) = m2 + 2m + 1 – m2 – m + 1 = m + 2
Phương trình đã cho có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ m + 2 > 0 ⇔ m > -2
Áp dụng hệ thức Vi-ét, ta có: 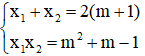
Do đó:
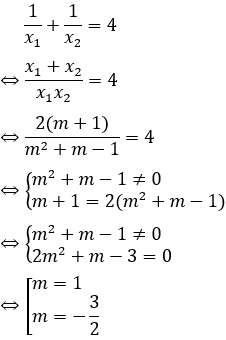
Kết hợp với điều kiện m > -2 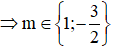 là các giá trị cần tìm.
là các giá trị cần tìm.
Bài 5: Cho phương trình 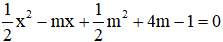 (m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm thỏa mãn
(m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm thỏa mãn 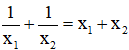
Giải:
Để phương trình đã cho có hai nghiệm phân biệt thì ∆ ≥ 0
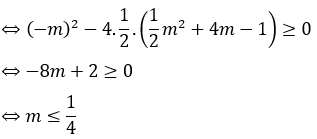
Phương trình có nghiệm khác 0 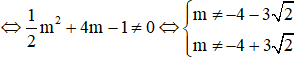
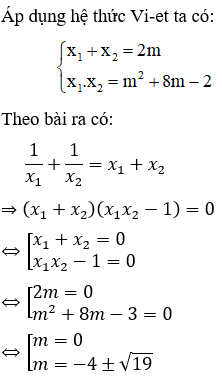
Kết hợp với điều kiện 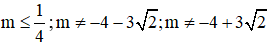 ta có
ta có
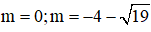
Vậy 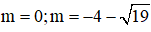 là các giá trị cần tìm.
là các giá trị cần tìm.
Bài 6: Cho phương trình 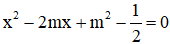 (m là tham số).
(m là tham số).
Tìm m để phương trình có hai nghiệm là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3.
Bài 7: Cho phương trình x2 – 2x – 2m2 = 0 với x là ẩn số.
Tìm giá trị của m để hai nghiệm của phương trình thỏa hệ thức x12 = 4x22.
Bài 8: Cho phương trình x2 – 5x + m = 0 (m là tham số).
Tìm m để phương trình trên có hai nghiệm x1, x2 thỏa mãn |x1 – x2| = 3.
Bài 9: Cho phương trình bậc hai x2 + 2(m – 1)x – (m + 1)= 0
Tìm giá trị m để phương trình có một nghiệm lớn hơn và một nghiệm nhỏ hơn 1.
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung giải trí học tập và các kiến thức thú vị khác tại đây.




