Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác

Cách tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay, chi tiết

Phương pháp giải

Để tìm giá trị lớn nhất, giá trị nhỏ nhất của một số hàm số lượng giác, ta biến đổi hàm số đã cho về dạng y = a + bsint hoặc y = a + bcost và sử dụng kết quả: – 1 ≤sinx ≤1; – 1 ≤cosx ≤1.

Bài tập minh họa có giải

Bài 1: Hàm số y = 2sinxcosx + cos2x có giá trị lớn nhất là

A. 3

B. 2√2

C. 2

D. √2

Lời giải:

Ta có

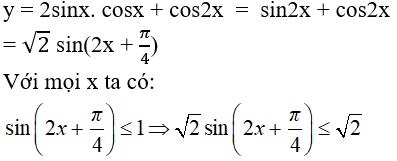
Vậy giá trị lớn nhất của hàm số là √2.

Đáp án là D.

Bài 2: Hàm số y = (sinx – cosx)² + cos2x có giá trị nhỏ nhất là:

A. – 1

B. 1- √2

C. 0

D. 1 + √2

Lời giải:

Ta có y = sin²x + cos²x -2sinxcosx + cos2x

= 1 – sin2x + cos2x = 1 – √2 sin(2x – π/4).

Với mọi x ta có:

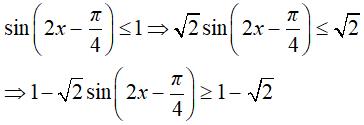
Từ đó suy ra giá trị nhỏ nhất của hàm số là 1 – √2.

Đáp án là B.

Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Mời các bạn cùng xem các nội dung học tập, giải trí và các kiến thức thú vị khác tại đây. Chúc các bạn lướt web vui vẻ !