Công thức tính chu vi hình thoi

Công thức tính chu vi diện tích các hình

I. Lý thuyết

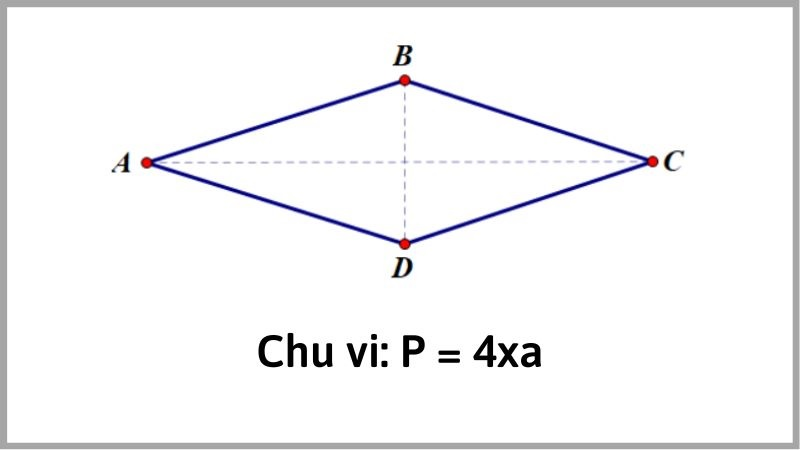
Công thức: Công thức tính chu vi hình thoi: Chu vi (P) của hình thoi được tính bằng công thức: P = 4a

trong đó là độ dài một cạnh của hình thoi.

II. Ví dụ minh họa

Ví dụ 1: Cho một hình thoi ABCD có độ dài cạnh là 8 cm, tính chu vi và diện tích của hình thoi này.

• Chu vi hình thoi được tính bằng công thức: 𝑃=4𝑎. Thay số vào, ta có: 𝑃=4×8=32 cm.
• Diện tích hình thoi được tính khi biết độ dài hai đường chéo, giả sử đường chéo dài 10 cm và ngắn 6 cm. Công thức tính diện tích là: 𝑆=12×𝑑1×𝑑2. Vậy diện tích là: 𝑆=12×10×6=30 cm².

Ví dụ 2: Một hình thoi có độ dài hai đường chéo là 14 cm và 8 cm, tính diện tích của hình thoi.

• Áp dụng công thức tính diện tích: 𝑆=12×𝑑1×𝑑2. Kết quả diện tích là: 𝑆=12×14×8=56 cm².

III. Bài tập vận dụng

Bài 1: Tấm bìa hình thoi có độ dài các cạnh bằng nhau và bằng 7 cm. Hỏi chu vi của tấm bìa hình thoi này bằng bao nhiêu?

Giải:

Ta có a = 7 cm.

Suy ra, chu vi của tấm bìa hình thoi là:

P = a x 4 = 7 x 4 = 28 (cm).

Bài 2: Tính chu vi của hình thoi biết độ dài cạnh = 5 dm

Giải:

Chu vi hình thoi đó là: 5 x 4 = 20 (dm)

Bài 3:Tính độ dài các cạnh của hình thoi ABCD khi biết chu vi hình thoi là 36 cm

Giải:

Gọi a là độ dài các cạnh của hình thoi.

P = a x 4 => a = P/4 = 36/4 = 9 (cm)

Đáp án: Độ dài một cạnh của hình thoi ABCD là 9 cm

Bài 4: Tính chu vi hình thoi biết các đường chéo bằng 16 cm và 30cm

Giải:

Gọi cạnh hình thoi bằng a, các đường chéo lần lượt là d1 và d2

– Áp dụng định lý Py – ta – go. Ta có: a2 = (d1/2)2 + (d2/2)2= (8)2 + (15)2 hay a = 17

Chu vi hình thoi: P = 4 x a = 68.

Bài 5: Tính chu vi của hình thoi biết độ dài cạnh = 15 dm.

Bài 6: Tính chu vi hình thoi ABCD khi biết độ dài cạnh là 7cm

Bài 7: Tính độ dài các cạnh của hình thoi ABCD khi biết chu vi hình thoi là 60cm

Bài 8: Tính chu vi hình thoi biết các đường chéo bằng 16 cm và 30cm