Để hàm số đồng biến trên R

Để hàm số đồng biến trên R

I. Lý thuyết

1. Khi nào thì đồng biến trên R?

– Hàm số đa thức bậc 1

Hàm số y = ax + b (a≠0) đồng biến trên ℝ khi và chỉ khi a > 0

– Hàm số bậc 3

Hàm số y=ax3+bx2+cx+d(a≠0) đồng biến trên ℝ khi và chỉ khi a>0△y’=b2-3ac≤0

Lưu ý: Hàm số đa thức bậc chẵn không thể đơn điệu trên R được, ví dụ như: Hàm số bậc 2, 4,…

2. Định lí

Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b). Khi đó hàm số sẽ đồng biến và nghịch biến với:

• Hàm số y = f(x) đồng biến trên khoảng (a;b) khi và chỉ khi f’(x) ≥ 0 với mọi giá trị x thuộc khoảng (a;b). Dấu bằng xảy ra tại hữu hạn điểm.

II. Ví dụ minh họa

Ví dụ 1: Cho hàm số f(x) = -2×3 + 3×2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?

A. Hàm số nghịch biến trên ℝ

B. f (a) > f (b)

C. f (b) < 0

D. f (a) < f (b)

Hướng dẫn giải: Chọn đáp án D.

Ta có: f’(x) = -6×2 + 6x – 3 < 0, ∀ x ∊ ℝ

⇒ Hàm số nghịch biến trên ℝ.

0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)

Ví dụ 2: Hàm số y = x3 – 3×2 + (m – 2) x + 1 luôn đồng biến khi:

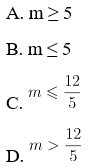
Hướng dẫn giải: Chọn đáp án A.

Ta có: y’ = 3×2 – 6x + m – 2

Hàm số đồng biến trên ℝ khi và chỉ khi y’ = 3×2 – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5

III. Bài tập vận dụng

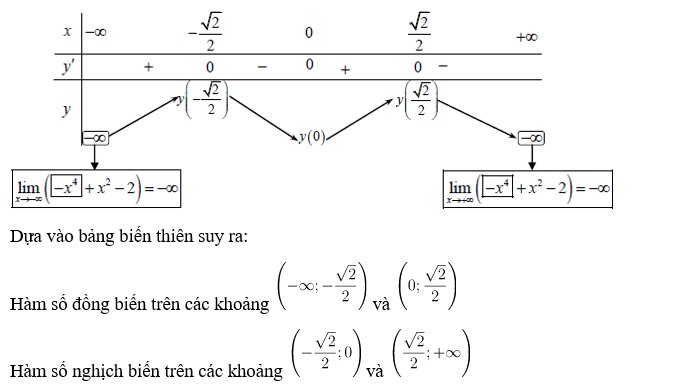
Bài 1: Xét tính đơn điệu của mỗi hàm số sau: y = -x4 + x2 – 2

Giải

Hàm số xác định với mọi x ∊ ℝ

y’ = -4×3 + 2x = 2x (-2×2 + 1)

Cho y’ = 0 ⇒ x = 0 hoặc x = -√2/2 hoặc x = √2/2

Bảng biến thiên:

Bài 2: Cho hàm số y=x³+2(m-1)x²+3x-2. Tìm m để hàm đã cho đồng biến trên R.

Giải:

Để y=x³+2(m-1)x²+3x-2 đồng biến trên R thì (m-1)²-3.3≤0⇔-3≤m-1≤3⇔-2≤m≤4.

Bài 3: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = ⅓ (m² – m) x³ + 2mx² + 3x – 2 đồng biến trên khoảng (-∞; +∞)?

A. 4

B. 5

C. 3

D. 0

Lời giải

Chọn A

y’ = (m² – m) x² + 4mx + 3

Hàm số đã cho đồng biến trên khoảng (-∞; +∞) ⇔ y’ ≥ 0 ∀ x ∊ ℝ.

+ Với m = 0 ta có y’ = 3 > 0, ∀ x ∊ ℝ ⇒ Hàm số đồng biến trên khoảng (-∞; +∞).

+ Với m = 1 ta có y’ = 4x + 3 > 0 ⇔ x > -¾ ⇒ m = 1 không thỏa mãn.

+ Với ta có y’ ≥ 0 ∀ x ∊ ℝ

Tổng hợp các trường hợp ta được -3 ≤ m ≤ 0

Vì m ∊ ℤ nên m ∊ {-3; -2; -1; 0}

Vậy có 4 giá trị nguyên của m thỏa mãn bài ra.

Bài 4: Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số sau đồng biến trên (–∞; +∞):

Lời giải

Ta có: y’ = (m – 1)x2 + 2mx + 3m – 2

Xét khi m = 1, ta có y’ = 2x + 1.

Nên hàm số đã cho không là hàm đồng biến trên (–∞; +∞).

⇒ m = 1 không thỏa mãn.

Xét khi m ≠ 1, ta có hàm số đồng biến trên (–∞; +∞).

Vậy: m ≥2.

Bài 5: Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số sau đồng biến trên R:

Lời giải

Ta có: y’ = mx2 – 4mx + 3m + 6

Trường hợp 1: Nếu m = 0 ⇒ y’ = 6 > 0, ∀x ∈ ℝ

⇒ Hàm số đồng biến trên ℝ nên m = 0 thỏa mãn.

Trường hợp 2: Nếu m ≠ 0, hàm số đã cho đồng biến trên ℝ.

Mà: m ∈ ℤ ⇒ m ∈ {1; 2; 3; 4; 5; 6}

Từ hai trường hợp trên ta được m ∈ {0; 1; 2; 3; 4; 5; 6}.

Bài 6: Cho hàm số y = f(x) = x3 + mx2 + 2x + 3. Tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ là:

Bài 7: Tìm các giá trị thực của m để hàm số đồng biến trên ℝ.

Bài 8: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ. Tổng giá trị của tất cả các phần tử thuộc S bằng