Đề kiểm tra 45 phút môn Toán (1 tiết) – Đề số 5 – Chương I – Giải Tích 12

Đề bài

Câu 1. Hàm số $y = {\left( {4 - {x^2}} \right)^2} + 1$ có giá trị lớn nhất trên đoạn [-1 ; 1] là :

A. 10                            B. 12            

C. 14                            D. 17

Câu 2. Đồ thị hàm số nào sau đây có ba đường tiệm cận ?

A. $y = {{1 - 2x} \over {1 + x}}$              

B. $y = {1 \over {4 - {x^2}}}$                     

C. $y = {{x + 3} \over {5x - 1}}$            

D. $y = {x \over {{x^2} - x + 9}}$

Câu 3. Cho hàm số y=f(x) xác định trên đoạn [a ; b]. Điều kiện đủ để hàm số nghịch biến tren đoạn [a ; b ] là

A. f(x) liên tục trên [a; b] và f’(x) < 0 với mọi $x \in (a;b)$.

B. f(x) liên tục trên (a ; b) và f’(x) > 0 với mọi $x \in [a;b]$.

C. $f'(x) \le 0$ với mọi $x \in [a;b]$

D. $f'(x) \ge 0$ với mọi $x \in [a;b]$.

Câu 4. Cho hàm số $y = a{x^4} + b{x^2} + c\,\,\,(a,b,c \in R)$ có đồ thị như hình vẽ sau.

 

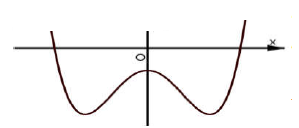
Số điểm cực trị của hàm số đã cho là: 

A. 2                           B. 3             

C. 0                           D. 1

Câu 5. Cho hàm số y = f(x) có bảng biến thiên như dưới đây. Tìm giá trị cực đại y_CĐ và giá trị cực tiểu y_CT của hàm số đã cho.

 

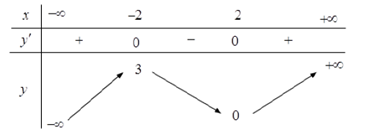
A. y_CĐ = 3 và y_CT = -2              

B. y_CĐ = 2 và y_CT = 0

C. y_CĐ = -2 và y_CT = 2                  

D. y_CĐ = 3 và y_CT = 0.

Câu 6. Cho hàm số y = f(x) có đồ thị như hình vẽ sau:

 

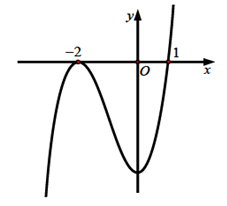
Tìm số nghiệm thực phân biệt của phương trình f(x) = 1.

A. 2                              B. 1         

C. 0                              D. 3

Câu 7. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 4m cắt đồ thị hàm số $y = {x^4} - 8{x^2} + 3$ tại bốn điểm phân biệt ?

A. $- {{13} \over 4} < m < {3 \over 4}$           

B. $- {{13} \over 4} \le m \le {3 \over 4}$              

C. $m \le {3 \over 4}$                     

D. $m \ge&nbsp; - {{13} \over 4}$.

Câu 8. Số điểm trên đồ thị hàm số $y = {{2x + 1} \over {x - 1}}$ có tọa độ nguyên là:

A. 5                               B. 3              

C. 4                               D. 2

Câu 9. Cho hàm số $y = {{2x + 1} \over {x - 2}}$. Khẳng định nào dưới đây là đúng ?

A. Đồ thị hàm số có tiệm cận đứng là x = 2.

B. Hàm số có cực trị.

C. Đồ thị hàm số đi qua điểm A(1 ; 3).

D. Hàm số nghịch biến trên $( - \infty ;2) \cup (2; + \infty )$.

Câu 10. Đồ  thị hàm số $y = {{2x - 1} \over {x - 3}}$y có bao nhiêu đường tiệm cận ?

A. 0                              B. 3              

C. 1                              D. 2

Câu 11. Cho hàm số $y = {{3x - 1} \over {3x + 2}}$. Đồ thị hàm số có đường tiệm cận ngang là:

A. y = 1                         B. x= 1   

C. y = 3                         D. x = 3.

Câu 12. Các khoảng đồng biến của hàm số $y = {x^3} + 3x$ là

A. $(0; + \infty )$                       

B. $(0;2)$                        

C. R                              

D $( - \infty ;1),\,(2; + \infty )$.

Câu 13. Đồ thị của hàm số $y =&nbsp; - {x^3} + 3{x^2} + 2x - 1$ và đồ thị hàm số $y = 3{x^2} - 2x - 1$ có tất cả bao nhiêu điểm chung ?

A. 0                               B. 2            

C. 3                               D. 1

Câu 14. Bảng biến thiên sau là của hàm số nào ?

A. $y = {x^3} - 3{x^2} + 3x$                          

B. $y =&nbsp; - {x^3} + 3{x^2} - 3x$

C. $y =&nbsp; - {x^3} - 3{x^2} - 3x$                        

D. $y = {x^3} + 3{x^2} - 3x$.

Câu 15. Cho hàm số $y = {{2x - 3} \over {4 - x}}$. Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Đồ thị hàm số trên không có điềm cực trị.

B. Giao điểm của hai tiệm cận là điểm I(- 2 ; 4).

C. Đồ thị hàm số trên có tiệm cận ngang x = 4.

D. Đồ thị hàm số trên có tiệm cận đứng y= - 2 .

Câu 16. Cho hàm số $y = x\ln x$. Chọn khẳng định sai trong số các khẳng định sau:

A. Hàm số đồng biến trên khoảng $(0; + \infty )$

B. Hàm số đồng biến trên khoảng $\left( {{1 \over e}; + \infty } \right)$.

C. hàm số có đạo hàm $y' = 1 + \ln x$.

D. Hàm số có tập xác định là $D = (0; + \infty )$.

Câu 17. Giá trị lớn nhất của hàm số $y = {x^3} - 3{x^2} - 9x + 10$ trên [- 2 ; 2] là:

A. 17                               B. – 15      

C. 15                               D. 5

Câu 18. Cho hàm số y = f(x) có bảng biến thiên như sau:

 

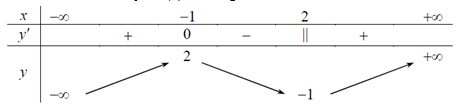
Mệnh đề nào dưới đây là sai ?

A. Hàm số không đạt cực tiểu tại điểm  x = 2.

B. Hàm số đạt cực đại tại điểm x = - 1 .

C. Điểm cực đại của đồ thị hàm số là (-1 ; 2).

D. Giá trị cực đại của hàm số là y = 2.

Câu 19. Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m + 1){x^4} - m{x^2} + 3$ có ba điểm cực trị.

A. $m \in ( - \infty ; - 1] \cup (0; + \infty )$         

B. $m \in ( - 1;0)$

C. $m \in ( - \infty ; - 1) \cup [0; + \infty )$            

D. $m \in ( - \infty ; - 1) \cup (0; + \infty )$

Câu 20. Hàm số $y = \sqrt {8 + 2x - {x^2}}$ đồng biến trên khoảng nào sau đây ?

A. $(1; + \infty )$                    B. $(1;4)$    

C. $( - \infty ;1)$                     D $( - 2;1)$.

Câu 21. Số điểm cực trị của hàm số $y = {(x - 1)^{2018}}$ là

A. 0                              B. 2018     

C. 2017                        D. 1

Câu 22. Số giao điểm của đường thẳng y= x + 2 và đồ thị hàm số $y = {{3x - 2} \over {x - 1}}$ là

A. 3                              B. 2   

C. 0                              D. 1

Câu 23. Điểm I(x₀; y₀) là tâm đối xứng của đồ thị hàm số y = f(x) nếu hàm số Y = g(x) qua phép tịnh tiến hệ tọc độ là:

A. Hàm số chẵn                

B. Hàm số không chẵn không lẻ

C. Hàm số lẻ                            

D. Hàm số vừa chẵn vừa lẻ.

Câu 24. Điều kiện để hàm số bậc ba không có cực trị là phương trình y’ = 0 có:

A. nghiệm kép          

B. Vô nghiệm           

C. Hai nghiệm phân biệt      

D. Cả A và B

Câu 25. Đường thẳng y = y₀ là tiệm cận ngang của đồ thị hàm số y = f(x) nếu:

A. $\left[ \matrix{\mathop {\lim }\limits_{x \to&nbsp; + \infty } y = {y_0} \hfill \cr \mathop {\lim}\limits_{x \to&nbsp; - \infty } y = {y_0} \hfill \cr}&nbsp; \right.$            

B. $\mathop {\lim }\limits_{x \to 0} y = {y_0}$             

C. $\mathop {\lim }\limits_{x \to&nbsp; - \infty } y =&nbsp; \pm \infty$         

D. $\left[ \matrix{\mathop {\lim }\limits_{x \to {y_0}^ + } y =&nbsp; + \infty&nbsp; \hfill \cr \mathop {\lim }\limits_{x \to {y_0}^ - } y =&nbsp; - \infty&nbsp; \hfill \cr}&nbsp; \right.$.

 

Lời giải chi tiết

Câu	1	2	3	4	5
Đáp án	D	B	A	B	D
Câu	6	7	8	9	10
Đáp án	B	A	C	A	D
Câu	11	12	13	14	15
Đáp án	A	C	C	A	A
Câu	16	17	18	19	20
Đáp án	A	C	A	D	D
Câu	21	22	23	24	25
Đáp án	A	B	C	D

Câu 1: D

$TX{\rm{D}}:D = R$

$\begin{array}{l}y = {\left( {4 - {x^2}} \right)^2} + 1\\y' = 2.\left( { - 2x} \right)\left( {4 - {x^2}} \right)\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x =&nbsp; - 2\end{array} \right.\end{array}$

$\begin{array}{l}f\left( 1 \right) = 10\\f\left( { - 1} \right) = 10\\f\left( 0 \right) = 17\end{array}$

Vậy $\max\,y=17$

Câu 2: B

$y = \dfrac{1}{{4 - {x^2}}}$

TXĐ:$D = R\backslash {\rm{\{ }}2, - 2\}$

$\begin{array}{l}\mathop {\lim }\limits_{x \to&nbsp; \pm \infty } \dfrac{1}{{4 - {x^2}}} = 0\\\mathop {\lim }\limits_{x \to&nbsp; \pm 2} \dfrac{1}{{4 - {x^2}}} = \infty \end{array}$

$\Rightarrow$  tiệm cận đứng là x=2 và x = -2, tiệm cận ngang là y=0

Câu 3:  A

Câu 4:  B

Câu 5:  D

Câu 6:  B

Câu 7:  A

Phương trình hoành độ giao điểm

$\begin{array}{l}{x^4} - 8{x^2} + 3 = 4m\\ \Leftrightarrow {x^4} - 8{x^2} + 3 - 4m = 0\left( * \right)\end{array}$

Đặt $t = {x^2}$ phương trình $\left( * \right)$ $\Leftrightarrow {t^2} - 8t + 3 - 4m = 0$ $\Leftrightarrow {t^2} - 8t + 3 - 4m = 0$

Để đồ thị và đường thẳng cắt nhau tại 4 điểm phân biệt thì phương trình ẩn t phải có 2 nghiệm dương phân biệt khác 0

$\begin{array}{l}\left\{ \begin{array}{l}\Delta ' = 13 + 4m > 0\\{t_1}{t_2} = 3 - 4m > 0\\{t_1} + {t_2} = 8 > 0\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}m > \dfrac{{ - 13}}{4}\\m < \dfrac{3}{4}\end{array} \right.\\ \Rightarrow \dfrac{{ - 13}}{4} < m < \dfrac{3}{4}\end{array}$

Câu 8:  C

TXĐ $x \ne 1$

$y = \dfrac{{2x + 1}}{{x - 1}} = \dfrac{{2\left( {x - 1} \right) + 3}}{{x - 1}}$$\, = 2 + \dfrac{3}{{x - 1}}$

Để số điểm trên đồ thị có tọa độ nguyên thì $\left[ \begin{array}{l}x - 1 = 1\\x - 1 =&nbsp; - 1\\x - 1 = 3\\x - 1 =&nbsp; - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\\x = 4\\x =&nbsp; - 2\end{array} \right.$

Vậy có 4 điểm.

Câu 9:  A

TXĐ: D=R\{2}

$\mathop {\lim }\limits_{x \to 2} \dfrac{{2x + 1}}{{x - 2}} = \infty$

Câu 10:  D

TXĐ: D=R\{3}

$\begin{array}{l}\mathop {\lim }\limits_{x \to&nbsp; \pm \infty } \dfrac{{2x - 1}}{{x - 3}} = 2\\\mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x - 1}}{{x - 3}} =&nbsp; + \infty \\\mathop {\lim }\limits_{x \to {3^ - }} \dfrac{{2x - 1}}{{x - 3}} =&nbsp; - \infty \end{array}$

Có 2 tiệm cận $y = 2,x = 3$.

Câu 11:  A

$TXD:D = R\backslash {\rm{\{ }}\dfrac{2}{3}{\rm{\} }}$

$\mathop {\lim }\limits_{x \to&nbsp; \pm \infty } \dfrac{{3x - 1}}{{3x + 2}} = 3$

Vậy TCN:  y=1.

Câu 12:  C

TXĐ: $D=R$

$\begin{array}{l}y = {x^3} + 3x\\ \Rightarrow y' = 3{x^2} + 3 > 0\forall x \in R\end{array}$

 

Vậy hàm số đồng biếm trên R.

Câu 13: C

Phương trình hoanh độ giao điểm là

$\begin{array}{l} - {x^3} + 3{x^2} + 2x - 1 = 3{x^2} - 2x - 1\\ \Leftrightarrow&nbsp; - {x^3} + 4x = 0\\ \Leftrightarrow&nbsp; - x\left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x =&nbsp; - 2\end{array} \right.\end{array}$

Câu 14: A

Câu 15: A

Câu 16: A

Câu 17: C

$TX{\rm{D}}:D = R$$TXD:D = R\backslash {\rm{\{ }}\dfrac{2}{3}{\rm{\} }}$

$\begin{array}{l}y = {x^3} - 3{x^2} - 9x + 10\\ \Rightarrow y' = 3{x^2} - 6x - 9\\y' = 0 \Leftrightarrow 3{x^2} - 6x - 9 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =&nbsp; - 1\end{array} \right.\end{array}$

$\begin{array}{l}f\left( { - 2} \right) = 8\\f\left( 2 \right) =&nbsp; - 12\\f\left( { - 1} \right) = 15\end{array}$

Vậy max y=15

Câu 18: A

Câu 19: D

 $y = (m + 1){x^4} - m{x^2} + 3$

TXĐ: $D = \mathbb{R}$

$y' = 4\left( {m + 1} \right){x^3} - 2mx$

$\begin{array}{l}y' = 0 \Leftrightarrow 4(m + 1){x^3} - 2mx = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{2m}}{{4m + 4}}{\rm{&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; (1)}}\end{array} \right.\end{array}$

Để pt $y = (m + 1){x^4} - m{x^2} + 3$ có 3 cực trị thì (1) có 2 nghiệm phân biệt

(1) $\Leftrightarrow$$\dfrac{{2m}}{{4m + 4}} > 0 \Leftrightarrow \left[ \begin{array}{l}m > 0\\m <&nbsp; - 1\end{array} \right.$

$\Rightarrow m \in \left( { - \infty , - 1} \right) \cup \left( {0, + \infty } \right)$

Câu 20: D

Câu 21: A

Câu 22: B

$\left\{ \begin{array}{l}x + 2 = \dfrac{{3x - 2}}{{x - 1}}\\x \ne&nbsp; - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 0\\x = 1\end{array} \right.$

Câu 23: C

Câu 24: D

Câu 25: A