Đề kiểm tra học kì 1 môn Toán lớp 9-Đề số 1 có đáp án

Đề bài

Bài 1: (2 điểm) 

1) Thực hiện phép tính:

a) $\sqrt 8  - 2\sqrt {18}  + 5\sqrt {32}  - \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}$

b) $\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7  - 1}} - \left( {\sqrt 5  + \sqrt 7 } \right)$

2) Giải phương trình: $x - \sqrt {x - 15}  = 17$.

Bài 2: (2,5 điểm) Cho biểu thức $P = \dfrac{{3x + \sqrt {9x}  - 3}}{{x + \sqrt x  - 2}} - \dfrac{{\sqrt x  + 1}}{{\sqrt x  + 2}} + \dfrac{{\sqrt x  - 2}}{{1 - \sqrt x }}$ với $x \ge 0,x \ne 1$

a) Rút gọn biểu thức $P$.

b) So sánh $P$ với $\sqrt P$ với điều kiện $\sqrt P$có nghĩa

c) Tìm $x$ để $\dfrac{1}{P}$ nguyên.

Câu 3: (2 điểm) (VD) Cho đường thẳng $\left( {{d_1}} \right)  :y = \left( {m - 1} \right)x + 2m + 1$.

a) Tìm $m$ để đường thẳng ${d_1}$ cắt trục tung tại điểm có tung độ là $- 3$. Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng $\left( d \right):y = x + 1$ nằm trên trục hoành.

b) Tìm $m$ để khoảng cách từ gốc tọa độ đến đường thẳng ${d_1}$ đạt giá trị lớn nhất.

Bài 4: (3 điểm)   Cho điểm M  bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của $\left( O \right)$ cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N.

a) Chứng minh $DC = DN$.

b) Chứng minh AC là tiếp tuyến của đường tròn tâm O.

c) Gọi H  là chân đường vuông góc kẻ từ M xuống AB, I  là trung điểm MH. Chứng minh B, C, I  thẳng hàng.

d) Qua O kẻ đường vuông góc với AB, cắt $\left( O \right)$ tại K  (K và M nằm khác phía với đường thẳng AB ). Tìm vị trí của M để diện tích tam giác MHK  lớn nhất.

Bài 5: (0,5 điểm)

            Cho các số thực dương $x,y,z$ thỏa mãn $x + 2y + 3z \ge 20$. Tìm giá trị nhỏ nhất của biểu thức : $A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}$.

Lời giải chi tiết

Bài 1:

1) Thực hiện phép tính:

$\begin{array}{l}a)\;\;\sqrt 8  - 2\sqrt {18}  + 5\sqrt {32}  - \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}} \\ = \sqrt {{2^2}.2}  - 2\sqrt {{3^2}.2}  + 5\sqrt {{4^2}.2}  - \left| {\sqrt 2  - 1} \right|\\ = 2\sqrt 2  - 2.3\sqrt 2  + 5.4\sqrt 2  - \left( {\sqrt 2  - 1} \right)\\ = 2\sqrt 2  - 6\sqrt 2  + 20\sqrt 2  - \sqrt 2  + 1\\ = 15\sqrt 2  + 1.\end{array}$

Vậy $\sqrt 8  - 2\sqrt {18}  + 5\sqrt {32}  - \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  = 15\sqrt 2  + 1$

$\begin{array}{l}b)\;\;\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7  - 1}} - \left( {\sqrt 5  + \sqrt 7 } \right)\\ = \dfrac{{\sqrt 5 .\sqrt 5  + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{\sqrt 7 .\sqrt 7  - \sqrt 7 }}{{\sqrt 7  - 1}} - \left( {\sqrt 5  + \sqrt 7 } \right)\\ = \dfrac{{\sqrt 5 \left( {6 + \sqrt 5 } \right)}}{{\sqrt 5 }} + \dfrac{{\sqrt 7 .\left( {\sqrt 7  - 1} \right)}}{{\sqrt 7  - 1}} - \sqrt 5  - \sqrt 7 \\ = 6 + \sqrt 5  + \sqrt 7  - \sqrt 5  - \sqrt 7  = 6.\end{array}$

Vậy $\dfrac{{5 + 6\sqrt 5 }}{{\sqrt 5 }} + \dfrac{{7 - \sqrt 7 }}{{\sqrt 7  - 1}} - \left( {\sqrt 5  + \sqrt 7 } \right) = 6$

2) Giải phương trình: $x - \sqrt {x - 15}  = 17$.

ĐKXĐ: $x \ge 15$

$\begin{array}{l}\;\;\;\;\;x - \sqrt {x - 15}  = 17\\ \Leftrightarrow x - 17 = \sqrt {x - 15} \\ \Leftrightarrow \left\{ \begin{array}{l}x - 17 \ge 0\\{\left( {x - 17} \right)^2} = {\left( {\sqrt {x - 15} } \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 17\\{x^2} - 34x + 289 = x - 15\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 17\\{x^2} - 35x + 304 = 0\end{array} \right.\end{array}$

 Xét phương trình bậc 2: ${x^2} - 35x + 304 = 0$ có: $\Delta  = {35^2} - 4.309 = 9 > 0$

Suy ra phương trình có hai nghiệm phân biệt $\left[ \begin{array}{l}{x_1} = \dfrac{{ - \left( { - 35} \right) + \sqrt 9 }}{{2.1}} = 19\;\;\;\left( {tm} \right)\\{x_2} = \dfrac{{ - \left( { - 35} \right) - \sqrt 9 }}{{2.1}} = 16\;\;\;\left( {ktm} \right)\end{array} \right.$

Vậy phương trình đã cho có nghiệm duy nhất là $x = 19$.

Bài 2:

Cho biểu thức $P = \dfrac{{3x + \sqrt {9x}  - 3}}{{x + \sqrt x  - 2}} - \dfrac{{\sqrt x  + 1}}{{\sqrt x  + 2}} + \dfrac{{\sqrt x  - 2}}{{1 - \sqrt x }}$  với $x \ge 0,x \ne 1$

a) Rút gọn biểu thức $P$.

ĐKXĐ: $x \ge 0,x \ne 1$

$\begin{array}{l}P = \dfrac{{3x + \sqrt {9x}  - 3}}{{x + \sqrt x  - 2}} - \dfrac{{\sqrt x  + 1}}{{\sqrt x  + 2}} + \dfrac{{\sqrt x  - 2}}{{1 - \sqrt x }}\\\;\;\; = \dfrac{{3x + \sqrt {9x}  - 3}}{{\left( {x - \sqrt x } \right) + \left( {2\sqrt x  - 2} \right)}} - \dfrac{{\sqrt x  + 1}}{{\sqrt x  + 2}} + \dfrac{{\sqrt x  - 2}}{{1 - \sqrt x }}\\\;\;\; = \dfrac{{3x + 3\sqrt x  - 3}}{{\left( {\sqrt x  + 2} \right).\left( {\sqrt x  - 1} \right)}} - \dfrac{{\left( {\sqrt x  - 1} \right).\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right).\left( {\sqrt x  + 2} \right)}} + \dfrac{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}{{ - \left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\\;\; = \dfrac{{3x + 3\sqrt x  - 3 - \left( {x - 1} \right) - \left( {x - 4} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \dfrac{{x + 3\sqrt x  + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\\;\; = \dfrac{{\left( {x + 2\sqrt x } \right) + \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\\;\; = \dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}.\end{array}$

Vậy$P = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}$.

b) So sánh $P$ với $\sqrt P$ với điều kiện $\sqrt P$có nghĩa

$\sqrt P$ có nghĩa $\Leftrightarrow \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}} \ge 0 \Leftrightarrow \sqrt x  - 1 > 0\;\;\left( {do\;\;\sqrt x  + 1 > 0\;\forall x \ge 0,\;\;x \ne 1} \right)$

                           $\Leftrightarrow \sqrt x  > 1 \Leftrightarrow x > 1.$

Xét hiệu: $P - \sqrt P  = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}} - \sqrt {\dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}}$.

$\begin{array}{l} \Rightarrow P - \sqrt P  = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}} - \sqrt {\dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}}  = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}} - \dfrac{{\sqrt {\sqrt x  + 1} }}{{\sqrt {\sqrt x  - 1} }}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}} - \dfrac{{\sqrt {\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)} }}{{{{\left( {\sqrt {\sqrt x  - 1} } \right)}^2}}} = \dfrac{{\sqrt x  + 1 - \sqrt {x - 1} }}{{\sqrt x  - 1}}.\end{array}$

Ta có: $\sqrt x  - \sqrt {x - 1}  = \dfrac{{\left( {\sqrt x  + \sqrt {x - 1} } \right)\left( {\sqrt x  - \sqrt {x - 1} } \right)}}{{\sqrt x  + \sqrt {x - 1} }}$$\,= \dfrac{{x - \left( {x - 1} \right)}}{{\sqrt x  + \sqrt {x - 1} }} = \dfrac{1}{{\sqrt x  + \sqrt {x + 1} }} > 0$

Mà có: $\sqrt x  - 1 > 0$ (cmt)

$\Rightarrow P - \sqrt P  > 0 \Rightarrow P > \sqrt P$ với mọi $x > 1.$

c) Tìm $x$ để $\dfrac{1}{P}$ nguyên.

Xét: $\dfrac{1}{P} = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 1}} = \dfrac{{\sqrt x  + 1 - 2}}{{\sqrt x  + 1}} = 1 - \dfrac{2}{{\sqrt x  + 1}}$.

Để $\dfrac{1}{P}$ nguyên thì $\dfrac{2}{{\sqrt x  + 1}}$ nguyên, suy ra $\sqrt x  + 1$ là ước của 2. Mà $\sqrt x  + 1 >$0

$\begin{array}{l} \Rightarrow \left( {\sqrt x  + 1} \right) \in U\left( 2 \right) \Rightarrow \left( {\sqrt x  + 1} \right) = \left\{ {1;\;2} \right\}.\\ \Rightarrow \left[ \begin{array}{l}\sqrt x  + 1 = 2\\\sqrt x  + 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = 1\\\sqrt x  = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\;\;\left( {ktm} \right)\\x = 0\;\;\;\left( {tm} \right)\end{array} \right..\end{array}$

Vậy với $x = 0$ thì $\dfrac{1}{P}$ nguyên.

 Câu 3:

Cho đường thẳng $\left( {{d_1}} \right)  :y = \left( {m - 1} \right)x + 2m + 1$.

a) Tìm $m$ để đường thẳng ${d_1}$ cắt trục tung tại điểm có tung độ là $- 3$. Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng $\left( d \right):y = x + 1$ nằm trên trục hoành.

Vì ${d_1}$ cắt trục tung tại điểm có tung độ là $- 3$, suy ra $\left( {0; - 3} \right)$ nằm trên đường thẳng ${d_1}$

$\Rightarrow  - 3 = \left( {m - 1} \right).0 + 2m + 1 \Leftrightarrow 2m =  - 4 \Leftrightarrow m =  - 2$.

Với $m =  - 2$ ta có phương trình đường thẳng $\left( {{d_1}} \right):y =  - 3x - 3$.

Nhận thấy: $A\left( {0; - 3} \right),\;B\left( { - 1;\;0} \right)$ nằm trên đồ thị hàm số. Vì hàm số $\left( {{d_1}} \right):y =  - 3x - 3$ là hàm số bậc nhất nên đồ thị của nó có dạng đường thẳng, từ đó ta có đồ thị:

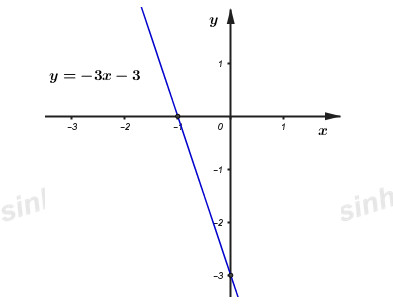
Hoành độ giao điểm của $\left( {{d_1}} \right):y =  - 3x - 3$ và $\left( d \right):y = x + 1$ là nghiệm của phương trình:

$x + 1 =  - 3x - 3 \Leftrightarrow 4x =  - 4$

$\Leftrightarrow x =  - 1 \Rightarrow y = x + 1 =  - 1 + 1 = 0$.

Vậy giao điểm của $\left( {{d_1}} \right):y =  - 3x - 3$ và $\left( d \right):y = x + 1$ là $\left( { - 1;0} \right)$. Nhận thấy điểm $\left( { - 1;0} \right)$ nằm trên trục hoành (do có tung độ bằng 0).

Vậy ta có điều cần chứng minh. 

b) Tìm $m$ để khoảng cách từ gốc tọa độ đến đường thẳng ${d_1}$ đạt giá trị lớn nhất.

+) Với $x = 0 \Rightarrow y = 2m + 1 \Rightarrow A\left( {0;2m + 1} \right)$ là giao điểm của ${d_1}$ với trục tung$\Rightarrow OA = \left| {2m + 1} \right|$

+) Với $y = 0 \Rightarrow x = \dfrac{{ - \left( {2m + 1} \right)}}{{m - 1}}$$\, \Rightarrow B\left( {\dfrac{{ - \left( {2m + 1} \right)}}{{m - 1}};0} \right)$ là giao điểm của ${d_1}$ với trục hoành

$\Rightarrow OB = \left| {\dfrac{{ - \left( {2m + 1} \right)}}{{m - 1}}} \right|$.

Từ O kẻ đường cao OH  với, ta được OH  chính là khoảng cách từ O tới ${d_1}$.

Xét tam giác vuông OAB vuông tại O có đường cao OH

$\Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}$ (hệ thức lượng trong tam giác vuông)

 Đặt $\dfrac{1}{{O{H^2}}} = t$ ta có:

$\begin{array}{l}t = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\\\;\; = \dfrac{1}{{{{\left( {2m + 1} \right)}^2}}} + \dfrac{{{{\left( {m - 1} \right)}^2}}}{{{{\left( {2m + 1} \right)}^2}}}\\\;\; = \dfrac{{{m^2} - 2m + 2}}{{4{m^2} + 4m + 1}}\;\;\;\left( {m \ne  - \dfrac{1}{2}} \right)\\ \Leftrightarrow 4{m^2}t + 4mt + t = {m^2} - 2m + 2\\ \Rightarrow {m^2}\left( {4t - 1} \right) + 2m\left( {2t + 1} \right) + t - 2 = 0\end{array}$

Coi đây là phương trình bậc 2 ẩn $m$, phương trình có nghiệm khi  

$\begin{array}{l}\Delta ' = {\left( {2t + 1} \right)^2} - \left( {4t - 1} \right)\left( {t - 2} \right) \ge 0\\ \Leftrightarrow 4{t^2} + 4t + 1 - 4{t^2} + 9t - 2 \ge 0\\ \Leftrightarrow 13t - 1 \ge 0 \Leftrightarrow t \ge \dfrac{1}{{13}}\\ \Rightarrow \dfrac{1}{{O{H^2}}} \ge \dfrac{1}{{13}} \Rightarrow OH \le \sqrt {13} \end{array}$

Dấu “=” xảy ra khi phương trình có nghiệm kép

$\Leftrightarrow m = \dfrac{{ - b}}{{2a}} = \dfrac{{ - \left( {4t + 2} \right)}}{{2\left( {4t - 1} \right)}} =  - \dfrac{{\dfrac{4}{{13}} + 2}}{{2.\left( {\dfrac{4}{{13}} - 1} \right)}} = \dfrac{5}{3}\;\;\;\left( {tm} \right)$.

Vậy $m = \dfrac{5}{3}$ là giá trị cần tìm.

Bài 4:

 

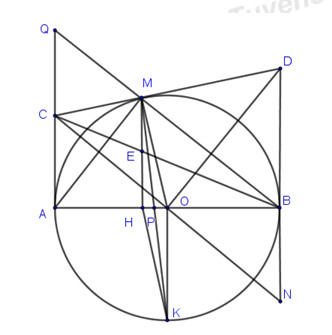
Cho điểm M bất kì trên đường tròn tâm O đường kính AB. Tiếp tuyến tại M và tại B của $\left( O \right)$ cắt nhau tại D. Qua O kẻ đường thẳng vuông góc với OD cắt MD tại C và cắt BD tại N.

a) Chứng minh $DC = DN$.

Xét đường tròn $\left( O \right)$ có MD và BD là tiếp tuyến với B, D là tiếp điểm

$\Rightarrow MD = DB$(tính chất tiếp tuyến)

Xét tam giác MOD và tam giác BOD có:

$MD = BD$ (cmt)

$MO = OB$ (cùng là bán kính đường tròn)

OD chung

$\Rightarrow \Delta MOD = \Delta BOD \Rightarrow \angle MDO = \angle BDO \Rightarrow OD$ là phân giác $\angle MDB$.

Xét tam giác CDN có:

OD là đường cao (do$OD \bot CN$)

OD là phân giác $\angle MDB$

Suy ra tam giác CDN cân tại D, suy ra $CD = ND$ (đpcm)

b) Chứng minh AC là tiếp tuyến của đường tròn tâm O.

Xét tam giác CND cân tại D có OD là đường cao ứng với đỉnh D, suy ra OD đồng thời là trung trực ứng với cạnh CN, suy ra $CO = ON$

Xét tam giác COA và tam giác BON có:

$CO = ON$ (cmt)

$OA = OB$ (do cùng là bán kính)

$\angle COA = \angle BON$ (hai góc đối đỉnh)

$\Rightarrow \Delta COA = \Delta BON \Rightarrow \angle CAO = \angle NBO = {90^o}$

Xét đường tròn tâm O có AC vuông góc với AO, AO là bán kính đường tròn, suy ra AC là tiếp tuyến của đường tròn (đpcm).

c) Gọi  H  là chân đường vuông góc kẻ từ M xuống AB, I  là trung điểm MH. Chứng minh B, C, I  thẳng hàng.

Kéo dài BM cắt AC tại Q, BC cắt MH  tại E

Xét tam giác BMD có $DM = DB\;\;\left( {cmt} \right) \Rightarrow \angle DMB = \angle DBM$

Ta có: $AB \bot AQ,\;\;AB \bot DN \Rightarrow AQ//DN.$

Mà có $\angle CQM = \angle MBD$ (so le trong)

Lại có: $\angle QMC = \angle DMB$ (đối đỉnh)

$\Rightarrow \angle CQM = \angle QMC$, suy ra tam giác MCQ cân tại C, suy ra $QC = MC$

Chứng minh tương tự như ở câu a ta có $AC = MC$ (do tính chất tiếp tuyến)

Suy ra $QC = AC \Rightarrow QC = \dfrac{1}{2}QA$.

Xét tam giác BQC có ME  song song với QC  (cùng vuông góc với AB)

$\Rightarrow \dfrac{{ME}}{{QC}} = \dfrac{{BM}}{{BQ}}$ (định lí Ta-lét)

Chứng minh tương tự có $\dfrac{{MH}}{{AQ}} = \dfrac{{BM}}{{BQ}}$

Suy ra  $\dfrac{{ME}}{{QC}} = \dfrac{{MH}}{{AQ}}$. Mà có $QC = \dfrac{1}{2}QA$ suy ra $ME = \dfrac{1}{2}MH$, suy ra E là trung điểm của MH.

Mà theo đề bài có I  là trung điểm của MH, suy ra I  trùng với E, suy ra B, C, I thẳng hàng (đpcm).

d) Qua O kẻ đường vuông góc với AB,  cắt $\left( O \right)$ tại K  (K và M nằm khác phía với đường thẳng AB). Tìm vị trí của M để diện tích tam giác MHK  lớn nhất.

Gọi P  là giao điểm của MK và AB.

Không mất tính tổng quát, ta chọn bán kính đường tròn bằng 1, giả sử độ dài đoạn $OH = a\;\;\left( {0 < a < 1} \right).$

$\Rightarrow MH = \sqrt {O{M^2} - O{H^2}}&nbsp; = \sqrt {1 - {a^2}}$.

Có MH song song với OK  (do cùng vuông góc với AB)

$\Rightarrow \dfrac{{PH}}{{PO}} = \dfrac{{MH}}{{OK}} = \dfrac{{\sqrt {1 - {a^2}} }}{1} \Rightarrow PH = \sqrt {1 - {a^2}} .OP.$

Ta có hệ:

$\left\{ \begin{array}{l}\dfrac{{PH}}{{PO}} = \sqrt {1 - {a^2}} \\PH + PO = OH = a\end{array} \right. \\\Rightarrow \left\{ \begin{array}{l}PO = \dfrac{{PH}}{{\sqrt {1 - {a^2}} }}\\PH + \dfrac{{PH}}{{\sqrt {1 - {a^2}} }} = a\end{array} \right.\\ \Rightarrow PH = \dfrac{{a.\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}}&nbsp; + 1}}\\ \Rightarrow OP = \dfrac{a}{{\sqrt {1 - {a^2}}&nbsp; + 1}}.$

Ta có:

$\begin{array}{l}{S_{MHK}} = {S_{MHP}} + {S_{PKH}} = \dfrac{1}{2}MH.HP + \dfrac{1}{2}OK.HP\\ = \dfrac{1}{2}\left( {\sqrt {1 - {a^2}} .\dfrac{{a\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}}&nbsp; + 1}} + 1.\dfrac{{a\sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}}&nbsp; + 1}}} \right)\\ = \dfrac{1}{2}a\sqrt {1 - {a^2}} .\dfrac{{\sqrt {1 - {a^2}}&nbsp; + 1}}{{\sqrt {1 - {a^2}}&nbsp; + 1}} = \dfrac{1}{2}a\sqrt {1 - {a^2}} .\end{array}$

Áp dụng bất đẳng thức Cosi ta có: $a\sqrt {1 - {a^2}}&nbsp; \le \dfrac{{{a^2} + 1 - {a^2}}}{2} = \dfrac{1}{2}$

Dấu “=” xảy ra $\Leftrightarrow a = \sqrt {1 - {a^2}}&nbsp; \Rightarrow a = \dfrac{1}{{\sqrt 2 }}$

$\Rightarrow \cos \angle MOH = \dfrac{{OH}}{R} = \dfrac{1}{{\sqrt 2 }} \Rightarrow \angle MOH = {45^o}$.

Vậy M là điểm nằm trên đường tròn sao cho $\angle MOH = {45^o}$ là điểm thỏa mãn yêu cầu bài toán.

Bài 5:

            Cho các số thực dương $x,\;y,\;z$ thỏa mãn $x + 2y + 3z \ge 20$. Tìm giá trị nhỏ nhất của biểu thức : $A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}$.

Ta có: $A = x + y + z + \dfrac{3}{x} + \dfrac{9}{{2y}} + \dfrac{4}{z}$$\, = \dfrac{1}{4}x + \left( {\dfrac{3}{4}x + \dfrac{3}{x}} \right) + \dfrac{1}{2}y + \left( {\dfrac{1}{2}y + \dfrac{9}{{2y}}} \right) + \dfrac{3}{4}z + \left( {\dfrac{1}{4}z + \dfrac{4}{z}} \right)$

Áp dụng bất đẳng thức Cosi cho các số dương ta có:

$\begin{array}{l} + )\dfrac{3}{4}x + \dfrac{3}{x} \ge 2\sqrt {\dfrac{3}{4}x.\dfrac{3}{x}}&nbsp; = 3\\ + )\dfrac{1}{2}y + \dfrac{9}{{2y}} \ge 2\sqrt {\dfrac{1}{2}y.\dfrac{9}{{2y}}}&nbsp; = 3\\ + )\dfrac{1}{4}z + \dfrac{4}{z} \ge 2\sqrt {\dfrac{1}{4}z.\dfrac{4}{z}}&nbsp; = 2\end{array}$

$\Rightarrow A \ge \dfrac{1}{4}\left( {x + 2y + 3z} \right) + 3 + 3 + 2 = \dfrac{{20}}{4} + 3 + 3 + 2 = 13$.

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{4}x = \dfrac{3}{x}\\\dfrac{1}{2}y = \dfrac{9}{{2y}}\\\dfrac{1}{4}z = \dfrac{4}{z}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\\z = 4\end{array} \right.$.

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại giaibaitap.pro.vn