Đề kiểm tra học kì 1 môn Toán lớp 9-Đề số 2 có đáp án

Đề bài

Bài 1: (3 điểm) . Thực hiện các phép tính

a) $2\sqrt {75}  - 3\sqrt {27}  - \dfrac{1}{4}\sqrt {192}$. 

b) $\sqrt {4 + 2\sqrt 3 }  + \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}$.

c) $\dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }}$. 

d) $\left( {\dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}} - \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 2}}} \right).\left( {\sqrt x  - \dfrac{4}{{\sqrt x }}} \right)\left( {x > 0;x \ne 4} \right)$.

Bài 2: (2 điểm) Cho hai hàm số bậc nhất $y =  - \dfrac{1}{2}x$ có đồ thị là $\left( {{d_1}} \right)$ và $y = 2x - 5$ có đồ thị là $\left( {{d_2}} \right)$

a) Vẽ $\left( {{d_1}} \right),\left( {{d_2}} \right)$ trên cùng hệ trục tọa độ.

b) Cho đường thẳng $\left( {{d_3}} \right):y = ax + b.$ Tìm $a,b$ để ${d_3}//{d_1}$ và cắt $\left( {{d_2}} \right)$ tại một điểm có tung độ bằng 3.

Bài 3: (1 điểm).Tìm $x$ biết $\sqrt {4x - 20}  = 7\sqrt {\dfrac{{x - 5}}{9}}  - 2$.

Bài 4: (0,5 điểm) Năm nay số dân ở một thành phố  A có 2 000 000 người. Hỏi 2 năm sau số dân của thành phố A là bao nhiêu người? Biết rằng bình quân mỗi năm số dân của thành phố A này tăng 0,5%.

Bài 5: (0,5 điểm) Các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ ${30^o}$. Tại thời điểm đó, bóng của một cái cây trên mặt đất dài $20m$. Hỏi cái cây đó cao bao nhiêu mét ? (làm tròn tới phần thập phân thứ nhất).

Bài 6: (3 điểm) Từ điểm $M$ nằm ở ngoài đường tròn $\left( {O,R} \right)$ với $OM > 2R$, vẽ hai tiếp tuyến $MA,MB\;\;(A,B$là hai tiếp điểm). Gọi $H$là giao điểm của $AB,OM$

a)Nếu cho $OM = R\sqrt 5$. Tính độ dài đoạn $MA$ theo $R$ và số đo $\angle AOM$ (làm tròn tới độ).

b)Chứng minh bốn điểm $M,A,O,B$ thuộc một đường tròn.

c)Gọi $AC$ là đường kính của đường tròn$\left( O \right)$, tia $CH$ cắt đường tròn $\left( O \right)$tại $N$. Chứng minh $4OH.OM = A{C^2}$.

d) Chứng minh rằng đường thẳng $AN$ đi qua trung điểm của $MH$

Lời giải chi tiết

Bài 1:

$\begin{array}{l}a)\;\;2\sqrt {75}  - 3\sqrt {27}  - \dfrac{1}{4}\sqrt {192}  = 2\sqrt {{5^2}.3}  - 3\sqrt {{3^2}.3}  - \dfrac{1}{4}\sqrt {{8^2}.3} \\\;\; = 2.5\sqrt 3  - 3.3\sqrt 3  - \dfrac{1}{4}.8\sqrt 3  =  - \sqrt 3 .\end{array}$.

Vậy $2\sqrt {75}  - 3\sqrt {27}  - \dfrac{1}{4}\sqrt {192}  =  - \sqrt 3$.

$\begin{array}{l}b)\;\;\sqrt {4 + 2\sqrt 3 }  + \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  \\\;\;\;= \sqrt {{{\left( {\sqrt 3 } \right)}^2} + 2\sqrt 3  + 1}  + \left| {\sqrt 3  - 2} \right|\\\;\;\; = \sqrt {{{\left( {\sqrt 3  + 1} \right)}^2}}  + \left| {\sqrt 3  - 2} \right| \\\;\;\;= \sqrt 3  + 1 + 2 - \sqrt 3  = 3.\;\;\;\left( {do\;\;2 > \sqrt 3 } \right)\end{array}$.

Vậy $\sqrt {4 + 2\sqrt 3 }  + \sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  = 3$.

$\begin{array}{l}c)\;\dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }} \\= \dfrac{{\sqrt 3 \left( {\sqrt 5  - \sqrt 4 } \right)}}{{\sqrt 5  - 2}} - \dfrac{{2 + \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}\\\;\; = \dfrac{{\sqrt 3 \left( {\sqrt 5  - 2} \right)}}{{\sqrt 5  - 2}} - \dfrac{{2 + \sqrt 3 }}{{{2^2} - {{\left( {\sqrt 3 } \right)}^2}}} \\= \sqrt 3  - \left( {2 + \sqrt 3 } \right) =  - 2.\end{array}$.

Vậy $\dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }} =  - 2$ .

$\begin{array}{l}d)\;\left( {\dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}} - \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 2}}} \right).\left( {\sqrt x  - \dfrac{4}{{\sqrt x }}} \right)\;\;\;\;\left( {x > 0;x \ne 4} \right)\\ = \left[ {\dfrac{{{{\left( {\sqrt x  - 2} \right)}^2}}}{{\left( {\sqrt x  - 2} \right).\left( {\sqrt x  + 2} \right)}} - \dfrac{{{{\left( {\sqrt x  + 2} \right)}^2}}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right].\left( {\sqrt x  - \dfrac{4}{{\sqrt x }}} \right)\\ = \dfrac{{x - 4\sqrt x  + 4 - x - 4\sqrt x  - 4}}{{x - 4}}.\dfrac{{x - 4}}{{\sqrt x }}\\ = \dfrac{{ - 8\sqrt x }}{{\sqrt x }} =  - 8.\end{array}$.

Vậy $\left( {\dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}} - \dfrac{{\sqrt x  + 2}}{{\sqrt x  - 2}}} \right).\left( {\sqrt x  - \dfrac{4}{{\sqrt x }}} \right) =  - 8$

Bài 2: (2 điểm) (VD)

Cho hai hàm số bậc nhất $y =  - \dfrac{1}{2}x$ có đồ thị là $\left( {{d_1}} \right)$ và $y = 2x - 5$ có đồ thị là$\left( {{d_2}} \right)$

a)      Vẽ $\left( {{d_1}} \right),\left( {{d_2}} \right)$ trên cùng hệ trục tọa độ.

Ta thấy :

+) $A\left( {0;0} \right),B\left( {2; - 1} \right)$ thuộc đồ thị hàm số $y =  - \dfrac{1}{2}x$ .

+) $B\left( {2; - 1} \right),C\left( {3;1} \right)$ thuộc đồ thị hàm số $y = 2x - 5$.

Từ đó ta có đồ thị của hai hàm số:

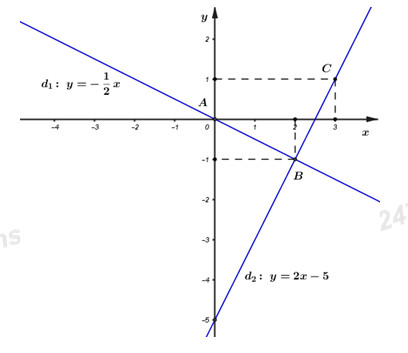
b)     Cho đường thẳng $\left( {{d_3}} \right):y = ax + b.$ Tìm $a,b$ để ${d_3}//{d_1}$ và cắt $\left( {{d_2}} \right)$ tại một điểm có tung độ bằng 3.

Vì  ${d_3}//{d_1}$ nên ta có: $a = \dfrac{{ - 1}}{2},\;\;b \ne 0 \Rightarrow {d_3}:\;\;y =  - \dfrac{1}{2}x + b.$

Theo đề bài $\left( {{d_3}} \right)$cắt $\left( {{d_2}} \right)$ tại một điểm có tung độ bằng $3 \Rightarrow 3 = 2x - 5 \Rightarrow x = 4$.

Suy ra $\left( {{d_3}} \right)$ đi qua điểm $M\left( {4;3} \right)$$\Rightarrow 4.\dfrac{{ - 1}}{2} + b = 3 \Rightarrow b = 5\;\;\left( {tm} \right).$

Vậy phương trình đường thẳng $\left( {{d_3}} \right)$là: $y =  - \dfrac{1}{2}x + 5$.

Bài 3:

Tìm $x$ biết $\sqrt {4x - 20}  = 7\sqrt {\dfrac{{x - 5}}{9}}  - 2$.

ĐKXĐ: $x \ge 5$

$\begin{array}{l}Pt \Leftrightarrow \sqrt {4x - 20}  = 7\sqrt {\dfrac{{x - 5}}{9}}  - 2\\ \Leftrightarrow \sqrt 4 .\sqrt {x - 5}  = 7.\sqrt {\dfrac{1}{9}} .\sqrt {x - 5}  - 2\\ \Leftrightarrow \dfrac{7}{3}\sqrt {x - 5}  - 2\sqrt {x - 5}  = 2\\ \Leftrightarrow \sqrt {x - 5}  = 6\\ \Leftrightarrow x - 5 = 36\;\;\;\left( {do\;\;6 > 0} \right)\\ \Leftrightarrow x = 41\;\;\left( {tm} \right).\end{array}$

Vậy $x = 41$ là nghiệm của phương trình.

Bài 4:

Năm nay số dân ở một thành phố  A có 2 000 000 người. Hỏi 2 năm sau số dân của thành phố A là bao nhiêu người? Biết rằng bình quân mỗi năm số dân của thành phố A này tăng 0,5%.

Cách 1: Áp dụng công thức trên ta có só dân của thành phố sau 2 năm là:

${P_2} = 2000000.{\left( {1 + 0,5\% } \right)^2} = 2020050$ người

Vậy sau 2 năm dân số của thành phố là 2020050 người.

Cách 2:

Dân số của thành phố A sau 1 năm là: $2000000 + 2000000.0,5\%  = 2010000$ người.

Dân số của thành phố A sau 2 năm là: $2010000 + 2010000.0,5\%  = 2020050$ người.

Vậy sau 2 năm dân số của thành phố là 2020050 người.

Bài 5:Các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ ${30^o}$. Tại thời điểm đó, bóng của một cái cây trên mặt đất dài $20m$. Hỏi cái cây đó cao bao nhiêu mét ? (làm tròn tới phần thập phân thứ nhất)

Ta có hình vẽ minh họa:

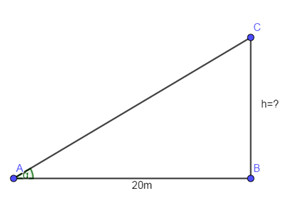
Trong đó đoạn thẳng AB là độ dài của bóng cây, đoạn BC là chiều cao của cây

Xét tam giác ABC vuông tại B có: $\tan \alpha  = \tan {30^o} = \dfrac{{BC}}{{AB}} = \dfrac{h}{{20}} \Rightarrow h = 20.\tan {30^o} = 11,5\left( m \right)$

Vậy chiều cao của cây là: $h = 11,5m$

Bài 6:Từ điểm $M$ nằm ở ngoài đường tròn $\left( {O,R} \right)$ với $OM > 2R$, vẽ hai tiếp tuyến $MA,MB\;\;(A,B$là hai tiếp điểm). Gọi $H$là giao điểm của $AB,OM$

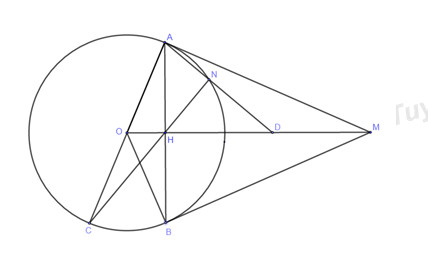
a)      Nếu cho $OM = R\sqrt 5$. Tính độ dài đoạn $MA$ theo $R$ và số đo $\angle AOM$ (làm tròn tới độ)

Xét tam giác OAM vuông tại A có:

+)  $A{M^2} + O{A^2} = O{M^2}$

$\Rightarrow AM = \sqrt {O{M^2} - O{A^2}}  = \sqrt {{{\left( {\sqrt 5 R} \right)}^2} - {R^2}}  = 2R$ (định lí Py-ta-go)

+)  $\cos \left( {\angle AOM} \right) = \dfrac{{OA}}{{OM}} = \dfrac{R}{{R\sqrt 5 }} = \dfrac{1}{{\sqrt 5 }}$

$\Rightarrow \angle AOM = \arccos \left( {\dfrac{1}{{\sqrt 5 }}} \right) \approx {63^o}$

b)     Chứng minh bốn điểm $M,A,O,B$ thuộc một đường tròn.

Xét đường tròn $\left( {O,R} \right)$ có: MA,MB là hai tiếp tuyến với A,B là tiếp điểm

$\Rightarrow \left\{ \begin{array}{l}OA \bot AM\\OB \bot BM\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle OAM = {90^o}\\\angle OBM = {90^o}\end{array} \right.$

Xét tứ giác MAOB có: $\angle OAM + \angle OBM = {90^o} + {90^o} = {180^o}$, suy ra tứ giác MAOB nội tiếp đường tròn, suy ra bốn điểm M,O,A,B cùng thuộc một đường tròn (đpcm).

c)Gọi $AC$ là đường kính của đường tròn$\left( O \right)$, tia $CH$ cắt đường tròn $\left( O \right)$tại $N$. Chứng minh:$4OH.OM = A{C^2}$.

Có $OA = OB$ (cùng là bán kính), suy ra O thuộc trung trực của AB.

Xét đường tròn $\left( {O,R} \right)$ có: MA,MB là hai tiếp tuyến với A,B là tiếp điểm, suy ra $MA = MB$, suy ra M thuộc trung trực của AB.

Từ hai điều trên ta được OM là trung trực của AB, suy ra OM vuông góc với AB tại H.

+) Xét tam giác vuông OAM vuông tại A có AH là đường cao

$\Rightarrow O{A^2} = OH.OM$ (hệ thức lượng trong tam giác vuông)

+) Mà có: $OA = \dfrac{1}{2}AC$ (do OA là bán kính, AC là đường kính)

$\Rightarrow {\left( {\dfrac{1}{2}AC} \right)^2} = OH.OM \Rightarrow A{C^2} = 4.OH.OM$ (đpcm).

d) Chứng minh rằng đường thẳng $AN$ đi qua trung điểm của $MH$.

Gọi D là giao điểm của AN và OM

Xét tam giác ADM và tam giác CHA có:

+) $\angle ACN = \angle MAD$ ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AN )

+) $\angle AMD = \angle CAH$ (do cùng phụ với $\angle HAM$)

$\Rightarrow \Delta ADM \sim \Delta CHA\;\;\left( {g - g} \right)$

$\Rightarrow \dfrac{{DM}}{{HA}} = \dfrac{{AD}}{{HC}} \Rightarrow DM = AD.\dfrac{{HA}}{{HC}}$                                (1)

Có AB vuông góc với OM (cmt) $\Rightarrow \angle AHD = {90^o}$

Có $\angle ANC$ là góc nội tiếp chắn nửa đường tròn $\Rightarrow \angle ANC = {90^o}$

Xét hai tam giác vuông HDN và ADH  có chung $\angle NDH$

$\Rightarrow \Delta HDN \sim \Delta ADH\;\left( {g - g} \right)$

$\Rightarrow \dfrac{{HD}}{{AD}} = \dfrac{{HN}}{{AH}} \Rightarrow HD = AD.\dfrac{{HN}}{{AH}}$.                                (2)

Xét tam giác AHC và tam giác NHB có:

+) $\angle AHC = \angle NHB$ (hai góc đối đỉnh)

+) $\angle CAH = \angle HNB$ (hai góc nội tiếp cùng chắn cung BC )

$\Rightarrow \Delta AHC \sim \Delta NHB\;\;\left( {g - g} \right) \Rightarrow \dfrac{{HN}}{{HA}} = \dfrac{{HB}}{{HC}}$

Mà có: $HA = HB$ (do OM là trung trực của AB) $\Rightarrow \dfrac{{HN}}{{HA}} = \dfrac{{HA}}{{HC}}$                        (3)

Từ (1) , (2) , (3) suy ra $HD = DM$, suy ra D là trung điểm của HM, suy ra AN đi qua trung điểm của HM(đpcm).

Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Hy vọng bài viết trên sẽ hữu ích và tác động tích cực tới kết quả học tập của bạn. Mời bạn tham khảo thêm các tài liệu học tốt khác tại đây .