Hướng dẫn giải chi tiết Đề thi vào lớp 10 có lời giải chi tiết hay nhất 2024 – Đề số : 02 dành cho học sinh tham khảo. Tuyển tập đề thi có đáp hay nhất được tổng hợp tại Giải Bài Tập.
Đề bài
Bài 1. (3,0 điểm)
1. Rút gọn biểu thức
2. Giải hệ phương trình
3. Giải phương trình
Bài 2. (2 điểm)
Cho hai hàm số: và có đồ thị lần lượt là và
1) Vẽ và trên cùng hệ trục tọa độ.
2) Bằng phép toán tìm tọa độ giao điểm của và
Bài 3. (1 điểm)
Cho phương trình (với m là tham số).
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Bài 4. (1,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.
Bài 5. (3 điểm).
Cho tam giác ABC vuông tại A , M là trung điểm của cạnh AC. Đường tròn đường kính MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.
1. Chứng minh tứ giác BADC nội tiếp.
2. Chứng minh DB là phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Lời giải chi tiết
Bài 1.
1. Rút gọn biểu thức
Ta có:
2. Giải hệ phương trình
Vậy hệ phương trình có nghiệm duy nhất là:
3. Giải phương trình
Ta có:
Khi đó phương trình đã cho có hai nghiệm phân biệt là:
Vậy tập nghiệm của phương trình đã cho là:
Bài 2: Cho hai hàm số: và có đồ thị lần lượt là và
1) Vẽ và trên cùng hệ trục tọa độ.
+) Vẽ đồ thị hàm số:
|
|
|
|
|
|
|
|
+) Vẽ đồ thị hàm số:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Đồ thị hàm số:
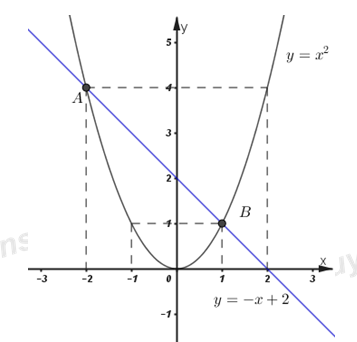
2) Bằng phép toán tìm tọa độ giao điểm của và
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt và
Bài 3:
1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có:
Vì
Hay phương trình luôn có hai nghiệm phân biệt với mọi
2) Tìm các số nguyên m để phương trình có nghiệm nguyên.
Phương trình đã cho luôn có hai nghiệm phân biệt với mọi
Đề bài yêu cầu tìm để Ta đưa bài toán về dạng tìm x nguyên để m nguyên.
Ta có:
Mà
Vậy với và thỏa mãn yêu cầu bài toán.
Bài 4.
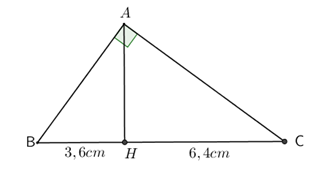
Ta có: nên :
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A với đường cao AH ta có:
Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
Vậy: BC = 10 cm; AH = 4,8 cm; AB = 6 cm; AC = 8 cm.
Bài 5.
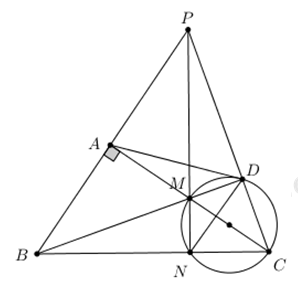
1. Chứng minh tứ giác BADC nội tiếp.
Ta có (góc nội tiếp chắn nửa đường tròn đường kính MC) .(Do B, M, D thẳng hàng)
Có (do giả thiết tam giác ABC vuông tại A)
Xét tứ giác BADC có Hai điểm A và D cùng nhìn BC dưới góc 900 Tứ giác BADC là tứ giác nội tiếp (Tứ giác có hai đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).
2. Chứng minh DB là phân giác của góc ADN.
Do BADC là tứ giác nội tiếp (cmt) (hai góc nội tiếp cùng chắn cung AB).
Lại có (hai góc nội tiếp cùng chắn cung MN của đường tròn đường kính MC).
là tia phân giác của góc ADN.
3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.
Ta có
Tam giác ABC vuông tại A
Xét tam giác PBC có là trực tâm tam giác PBC.
.
Lại có (góc nội tiếp chắn nửa đường tròn đường kính MC)
Qua điểm M nằm ngoài đường thẳng BC ta kẻ được và
hay ba điểm P, M, N thẳng hàng.
Giaibaitap.pro.vn
Cảm ơn bạn đã theo dõi bài viết tại Giải Bài Tập. Hy vọng bài viết trên sẽ hữu ích và tác động tích cực tới kết quả học tập của bạn. Mời bạn tham khảo thêm các tài liệu học tốt khác tại đây.